CENTROID OF TRIANGLE WITH 3 VERTICES

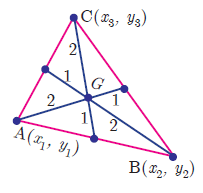
The coordinates of the centroid (G) of a triangle with vertices

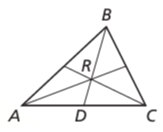
The centroid R of a triangle is two thirds of the distance from each vertex to the midpoint of the opposite side.

To find centroid of the triangle with three vertices, we use the formula

= (x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3

Find the coordinates of the centroid of the triangle with the given vertices.

Problem 1 :

A(2, 3), B(8, 1), C(5, 7)

Solution :

Let the given points as (x₁, y₁), (x₂, y₂) and (x₂, y₂) are vertices of triangle.

Centroid =  (x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3

= (2 + 8 + 5)/3, (3 +  1 + 7)/3

= 15/3, 11/3

= (5, 11/3)

Problem 2 :

F(1, 5), G(−2, 7), H(−6, 3)

Solution :

Let the given points as (x₁, y₁), (x₂, y₂) and (x₂, y₂) are vertices of triangle.

Centroid =  (x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3

= (1 - 2 - 6)/3, (5 + 7 + 3)/3

= -7/3, 15/3

= (-7/3, 5)

Problem 3 :

S(5, 5), T(11, −3), U(−1, 1)

Solution :

Let the given points as (x₁, y₁), (x₂, y₂) and (x₂, y₂) are vertices of triangle.

Centroid =  (x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3

= (5 + 11 - 1)/3, (5 - 3 + 1)/3

= 15/3, 3/3

= (5, 1)

Problem 4 :

X(1, 4), Y(7, 2), Z(2, 3)

Solution :

Let the given points as (x₁, y₁), (x₂, y₂) and (x₂, y₂) are vertices of triangle.

Centroid =  (x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3

= (1 + 7 + 2)/3, (4 + 2 + 3)/3

= 10/3, 9/3

= (10/3, 3)

The point D is the centroid of △ABC. Find CD and CE.

Problem 5 :

Find the third vertex of triangle, if its two vertices are (–4, 1) and (5, 2) and its centroid is (1, 3).

Solution :

Let (x, y) be the third vertex.

Centroid =  (x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3

(–4, 1) and (5, 2) and (x, y)

(-4 + 5 + x)/3, (1 + 2 + y)/3 = (1, 3)

(1 + x)/3, (3 + y)/3 = (1, 3)

Equating x and y coordinates, we get

So, the missing point is (2, 6).

Problem 6 :

The co-ordinates of the mid points of the sides of a triangle are (1, 1) , (2, –3) and (3, 4). Find The co-ordinates of its centroid.

Solution :

Let A(x₁, y₁) B(x₂, y₂) and C(x₃, y₃) are three vertices of the triangle.

Midpoint of the side AB = (1, 1)

Midpoint of the side BC = (2, -3)

Midpoint of the side CA = (3, 4)

Midpoint of the side AB :

(x₁ + x₂)/2, (y₁ + y₂)/2 = (1, 1)

Equating x and y-coordinates, we get

Midpoint of the side BC :

(x₂ + x₃)/2, (y₂ + y₃)/2 = (2, -3)

Equating x and y-coordinates, we get

Midpoint of the side CA :

(x₃ + x₁)/2, (y₃ + y₁)/2 = (3, 4)

Equating x and y-coordinates, we get

(1) + (3) + (5)

x₁ + x₂ + x₂ + x₃ + x₃ + x₁ = 2 + 4 + 6

2x₁ + 2x₂ + 2x₃ = 12

x₁ + x₂ + x₃ = 6 ------(7)

Applying (1) in (7), we get

2 + x₃ = 6

x₃ = 6 - 2

x₃ = 4

Applying the value of x₃ in (3), we get

x₂ + 4 = 4

x₂ = 4 - 4

x₂ = 0

Applying the value of x₂ in (1), we get

x₁ + 0 = 2

x₁ = 2

(2) + (4) + (6)

y₁ + y₂ + y₂ + y₃ + y₃ + y₁= 2 - 6 + 8

2y₁ + 2y₂ + 2y₃ = 4

y₁ + y₂ + y₃ = 2  -----(8)

Applying (2) in (8), we get

2 + y₃  = 2

y₃  = 2 - 2

y₃  = 0

By applying the value of y₃ in (4), we get

y₂ + 0 = -6

y₂ = -6

By applying the value of y₂ and y₃ in (8), we get

y₁ + (-6) + 0 = 2

y₁ = 2 + 6

y₁ = 8

So, the required points are (2, 8) (0, -6) and (4, 0)

Centroid = (2 + 0 + 4)/3, (8 -  6 + 0)/3

= (6/3), (2/3)

= (2, 2/3)