CENTRAL ANGLES OF A CIRCLE

For each figure, determine the indicated measures.

Problem 1:

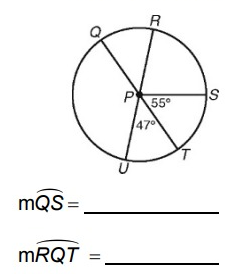
Solution :

measure of arc QS = 180˚ - mST

measure of arc QS = 180˚ - 55˚

measure of arc QS = 125˚

measure of arc RS = 180˚ - m ST - m TU

= 180˚ - 47˚ - 55˚

measure of arc RS = 78˚

measure of arc RQT = 360˚ - measure of arc ST - measure of arc RS

= 360˚ - 55˚ - 78˚

measure of arc RQT = 227˚

Problem 2 :

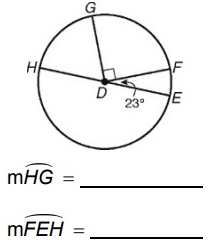
Solution :

measure of arc HG = 180 - 90˚ - 23˚

measure of arc  HG = 67˚

measure of arc  FEH = 180˚ + 23˚

m FEH = 203˚

Problem 3 :

Find the value of x.

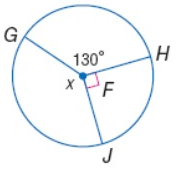
Solution :

m∠GFH + m∠HFJ + m∠GFJ = 360˚

130˚ + 90˚ + m∠GFJ = 360˚

220˚ = m∠GFJ = 360˚

m∠GFJ = 360˚ - 220˚

m∠GFJ = 140˚

So, value of x is 140˚.

Problem 4 :

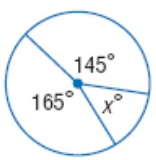
Solution :

165˚ + 145˚ + x = 360˚

310˚ + x = 360˚

x = 360˚ - 310˚

x = 50˚

So, value of x is 50˚.

Problem 5 :

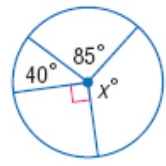
Solution :

40˚ + 85˚ + 90˚ + x˚ = 360˚

215˚ + x˚ = 360˚

x = 360˚ - 215˚

x = 145˚

So, value of x is 145˚.

Problem 6 :

i)  Find measure of arc ED

ii)  Measure of arc COB

iii)  Measure of AB

iv)  Measure of arc BOE.

Solution :

i)  measure of ED :

m ED = 90˚ - 15˚

m ED = 75˚

ii)  m∠COB :

m∠COB = 360˚ - 90˚ - 75˚ - 15˚ - 15˚

= 360˚ - 195˚

m∠COB = 165˚

iii) m AB :

m AB = 360˚ - (90˚ + 75˚ + 15˚ + 165˚)

= 360˚ - 345˚

m AB = 15˚

iv) m∠BOE :

m∠BOE = 90˚ + 15˚

m∠BOE = 105˚

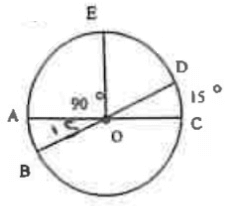
Problem 7 :

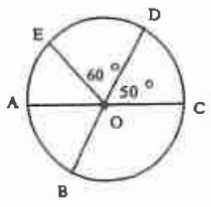
i) Measure of arc AE

ii) Measure of AB

iii) Measure of arc ECB

iv) Measure of arc BOC

Solution :

measure of arc AE :

m AE = 180˚ - 60˚ - 50˚

m AE = 70˚

measure of arc AB :

m AB = 180˚ - 60˚ - 70˚

m AB = 50˚

measure of arc ECB :

m ECB = 360˚ - m EAB

= 360˚ - (m AE + m AB)

= 360˚ - (70˚ + 50˚)

m ECB = 240˚

measure of arc ∠BOC :

m∠BOC = 180˚ - ∠DOC

= 180˚ - 50˚

m∠BOC = 130˚

Problem 8 :

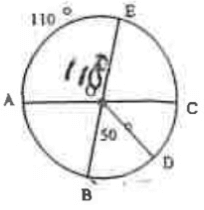
i) Find measure of arc DC.

ii) Measure of EAB

iii) Measure of ACB

iv) Measure of AOB.

Solution :

measure of arc DC :

m DC = m∠COB

= 110˚ - 50˚

m DC = 60˚

measure of arc EAB :

m EAB = 180˚ - 110˚

m EAB = 70˚

m ACB :

m ACB = 180˚ + 110˚

m ACB = 290˚

m∠AOB :

m∠AOB = 180˚ - 110˚

m∠AOB = 70˚