CALCULUS OPTIOMIZATION PRACTICE PROBLEMS

Problem 1 :

When a small business employs x workers to manufacture its goods, the profit made is given by

P(x) = -2x³ + 2400 x - 4000 euros per week.

a) How many employees should they use to maximise profit ?

b) What is the maximum profit ?

Solution :

P(x) = -2x³ + 2400 x - 4000

P'(x) = -2(3x²) + 2400(1) - 0

P'(x) = -6x² + 2400

P'(x) = 0

-6x² + 2400 = 0

-6x² = - 2400

x² = 400

x = 20

Finding the second derivative :

P'(x) = -6x² + 2400

P''(x) = -6(2x) + 0

= -12x

When x = 20, P''(20) = -12(20)

= -240 < 0

Then maximum at x = 20

a)  Number of employees required to maximize the profit is 20.

b)  P(x) = -2x³ + 2400 x - 4000

P(20) = -2(20)³ + 2400 (20) - 4000

= -2(8000) + 48000 - 4000

= -16000 + 48000 - 4000

= 28000

The maximum profit is 28000 euros.

Problem 2 :

Square corners are cut from a piece of 12 cm by 12 cm tinplate which is then bent to form an open dish. What size squares should be removed to maximise the capacity of the dish ?

Solution :

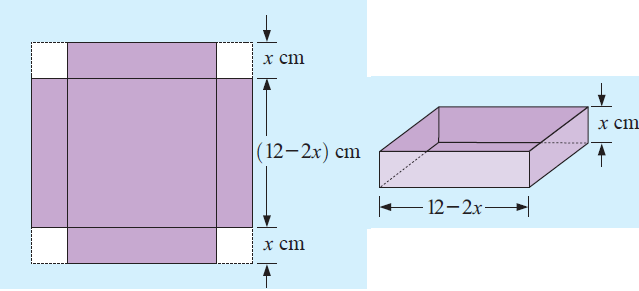
Capacity of the dish = length x width x height

length = 12 - 2x, width = 12 - 2x and height = x

Capacity = (12 - 2x)(12 - 2x) x

f(x) = x(12 - 2x)²

f'(x) = x(2(12-2x))(-2) + (1) (12 - 2x)²

= -4x (12-2x) + (12 - 2x)²

f'(x) = (12 - 2x) [-4x + 12 - 2x]

= (12 - 2x) [-6x + 12]

f'(x) = 0

(12 - 2x) (12 - 6x) = 0

x = 6, x = 2

f'(x) = (12 - 2x) [-6x + 12]

f'(x) = (12 - 2x) (-6) + (-6x + 12) (-2)

= -72 + 12x + 12x - 24

f''(x) = - 86 + 24x

Applying the values of x one by one.

The maximum capacity occurs when x = 2 cm, we should cut out 2 cm squares.

Problem 3 :

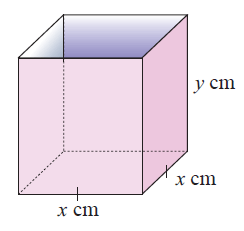
An open rectangular box has a square base, and its outer surface area must be 108 cm²

a) Find the equation in terms of x and y.

b) Write y in terms of x.

c) Find the formula for the capacity C in terms of x and y.

d) What size must the base be in order to maximise the capacity ?

Solution :

a) Surface area of the square base cube = 4a²

Area of four faces + area of bottom face = 108

4xy + x² = 108

b) Solving for y in terms of x,

4xy = 108 - x²

y = (108 - x²)/4x

y = (108/4x) - (x²/4x)

y = (27/x) - (x/4)

c) Capacity of the cube = length x width x height

= x ⋅ x ⋅ y

= x²[(27/x) - (x/4)]

= 27x - (x ⋅x² /4)

= 27x - (x³/4)

d)  f(x) =  27x - (x³/4)

f'(x) = 27 - 3x²/4

Put f'(x) = 0

27 - 3x²/4 = 0

3x²/4 = 27

x² = 27(4/3)

x² = 36

x = 6

f''(x) = 0 - 6x/4

f''(x) = -3x/2

f''(6) = -18/2

= -9 < 0 maximum

At x = 6, the area will be maximised.

Problem 4 :

The slant edge of the cone has length 12 cm. If the cone has height x cm, find 

a) an expression for the volume of the cone in terms of x.

b) The value of x for which the cone has the maximum possible volume.

Solution :

Here height of the cone is x cm.

Volume of cone = 1/3 π r² h

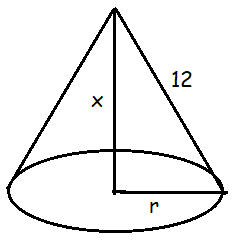
a)  Volume of cone = 1/3 π r² x

r² = 12² - x²

r² = 144 - x²

V (x) = 1/3 π(144 - x²) ⋅ x

V (x) = 1/3 π(144x - x³)

b)  V (x) = 1/3 π(144x - x³)

V' (x) = 1/3 π(144 - 3x²)

V' (x) = 0

1/3 π(144 - 3x²) = 0

144 - 3x² = 0

3x² = 144

x² = 48

x = 4√3

Applying x = 4√3 in second derivative,

V'' (x) = 1/3 π(0 - 6x)

V'' (x) = -2xπ

V'' (4√3) = -2(4√3)π

= -8√3π < 0 maximum

To find the maximum value, we apply x = 4√3 in the original function.

V (x) = 1/3 π(144(4√3) - (4√3)³)

= 1/3 π(576√3 - 192√3)

= 1/3 π(384√3)

= 128π

Maximizing the volume at x = 4√3 and the volume is 128π cubic units.