CALCULATING THE MEAN FROM A FREQUENCY TABLE

Work out the mean for each of these frequency tables, you may not use calculator.

Problem 1 :

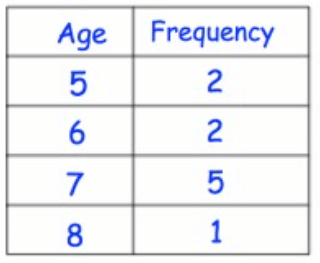
Solution :

From the table, we understand that,

• at the age of 5 we have 2 people
• at the age of 6 we have 2 people
• at the age of 7 we have 5 people
• at the age of 8 we have 1 people

To find the total number of people, we will add 2, 2, 5 and 1.

Problem 2 :

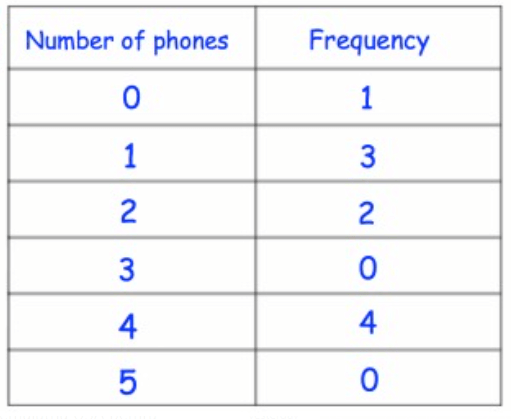
Solution :

From the table, we understand that,

• 1 person is having no phone (0 phones)
• 3 persons is having 1phone.
• 2 persons is having 2 phones.
• No person is having 3 phones.
• 4 persons is having 4 phones.
• No person is having 5 phones.

Problem 3 :

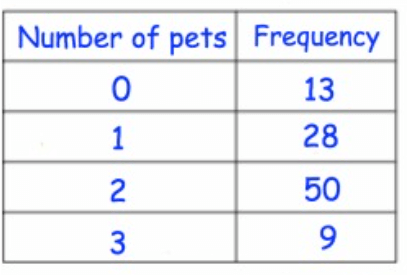
Solution :

Problem 4 :

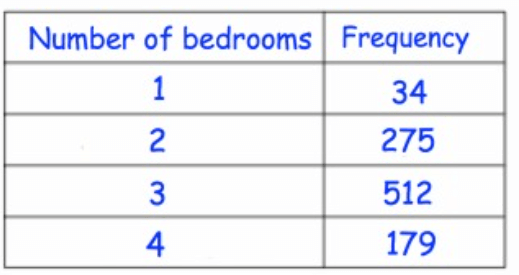
Solution :

Problem 5 :

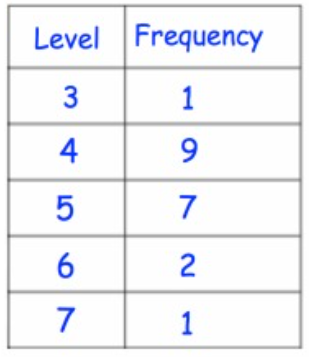
Solution :

Problem 6 :

The tale below shows the data on the heights in cm of 51 children.

a) Estimate the mean

b) Estimate the median height

c) Find the modal class

Solution :

a) Calculating the mean :

ΣMF = 870 + 2480 + 3465 + 1400

= 8215

ΣF = 6 + 16 + 21 + 8

= 51

Mean = ΣMF/ΣF

= 8215 / 51

= 161

b) Finding median :

ΣF = 51

Median value = 51/2

= 25.5

26th value will be the median.

26th value lies in the interval 160 ≤ h < 170, in this interval 4th value will be the median.

= 160 + (4/21) x 10

= 160 + (40/21)

= 160 + 1.9

= 161.9

Approximately 162 is the median.

c) Finding mode :

The high frequency is in the interval 160 ≤ h < 170 and this is the modal class.

Problem 6 :

The age of children in a primary school were recorded in the table below.

a) Estimate the mean

b) Estimate the median

c) Estimate the modal class

Solution :

a) Calculating mean :

ΣMF = 36 + 88 + 130 + 72 + 69

= 395

ΣF = 12 + 11 + 10 + 4 + 3

= 40

Mean = ΣMF/ΣF

= 395 / 40

= 9.875

b) Finding median :

ΣF = 40

Median value = 40/2

= 20

20^th value will be the median.

20^th value lies in the interval 6 to 10, in this interval we have 11 values 

= 5.5 + (8.5/11) x 3

= 5.5 + 0.77 x 3

= 5.5 + 2.31

= 7.81

7.81 is the median.

c) Finding mode :

Highest frequency is in the interval 6 - 10, then this is the modal class.