CALCULATE MISSING FREQUENCY WHEN MEAN IS GIVEN

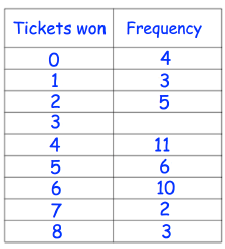
Problem 1 :

Aidan plays 50 games in an arcade. The table shows how many tickets he won in each game.

(a) Work out the missing frequency

(b) Work out the total number of tickets won

(c) Work out the mean number of tickets won per game.

Aidan wants to exchange his ticket for a prize that costs 800 tickets.

(d) How many more games do you expect Aidan would have to play?

Solution :

Let x be the missing frequency.

a) Total number of games played = 50

4 + 3 + 5 + x + 11 + 6 + 10 + 2 + 3 = 50

12 + x + 32 = 50

44 + x = 50

x = 50 - 44

x = 6

b) Number of tickets won =

0(4) + 1(3) + 2(5) + 3x + 4(11) + 5(6) + 6(10) + 7(2) + 8(3)

= 0 + 3 +10 + 3x + 44 + 30 + 60 + 14 + 24

= 13 + 3x + 172

= 185 + 3x

= 185 + 3(6)

= 185 + 18

= 203

c)  Mean number of tickets = 203 / 50

= 4.06

d)  800 - 203

= 597

= 597/4.06

= 147

Expected number of games = 147.

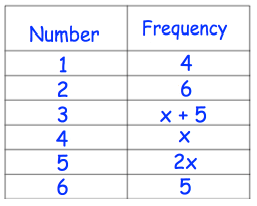
Problem 2 :

Max rolls a dice 80 times. The table shows the results.

(a) Find the value of x

(b) Work out the mean score

Solution :

Number of times he rolls the dice = 80

4 + 6 + x + 5 + x + 2x + 5 = 80

20 + 4x = 80

4x = 80 - 20

4x = 60

x = 60/4

x = 15

b) Mean = 80/6

= 13.3

Problem 3 :

A student was asked to find the arithmetic mean of the numbers 3, 11, 7, 9, 15, 13, 8, 19, 17, 21, 14 and x. He found the mean to be 12. What should be the number in the place of x ?

Solution :

Mean = 12

(3+11+7+9+15+13+8+19+17+21+14+x) / 12 = 12

137 + x = 144

x = 144 - 137

x = 7

Problem 4 :

The average of 2, 7, 6 and x is 5 and the average of 18, 1, 6, x and y is 10. What is the value of y.

Solution :

Let {2, 7, 6, x} be the first data set

Average = 5

(2 + 7 + 6 + x)/4 = 5

15 + x = 20

x = 20 - 15

x = 5

Let {18, 1, 6, x and y is 10} be the second data set.

(18 + 1 + 6 + x + y + 10)/6 = 10

35 + x + y = 60

Applying the value of x,

35 + 5 + y = 60

40 + y = 60

y = 60 - 40

y = 20

So, the missing values are x = 5 and y = 20.

Problem 5 :

If the mean of 5 observations x, x + 2, x + 4, x + 6 and x + 8 is 11, then the mean of the last three observation is.

Solution :

Mean of 5 observations = 11

(x + x + 2 + x + 4 + x + 6 + x + 8) / 5 = 11

5x + 20 = 55

5x = 55 - 20

5x = 35

x = 35/5

x = 7

Mean of last three observations :

= (x + 4 + x + 6 + x + 8)/3

= (3x + 18)/3

= [3(7) + 18] / 3

= (21 + 18)/3

= 39/3

= 13