BOUNDED AND UNBOUNDED INTERVALS

Problem 1 :

Convert interval notation to inequality notation or vice versa. Find the endpoints and state whether the interval is bounded, its type, and graph the interval.

(a)  [-6, 3)

(b)  (-∞, -1)

(c)  -2 ≤ x ≤ 3

Solution :

(a) It has endpoints -6 and 3.

Inequality Notation :

The possible values are -6 ≤ x < 3. 

Graph :

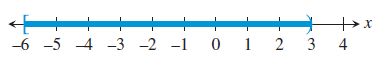
Type of interval :

It is bounded.

(b)  (-∞, -1)

Endpoints :

It has the endpoint -1.

Inequality Notation :

The possible values are x < -1. 

Graph :

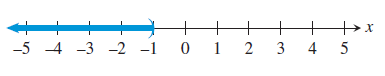
Type of interval :

It is unbounded.

(c)  -2 ≤ x ≤ 3

Endpoints :

-2 and 3 are the endpoints.

Inequality Notation :

The possible values are -2 ≤ x ≤ 3. 

Graph :

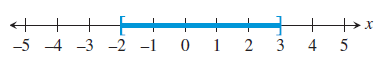
Type of interval :

It is bounded.

Problem 2 :

Describe and graph the interval of real numbers.

(i) x ≤ 2

(ii) -2 ≤ x < 5

Solution :

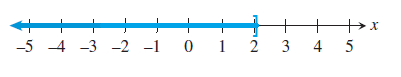
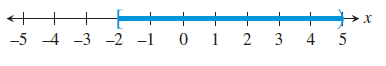
Problem 3 :

Write the following as interval notation :

(i) (-∞, 7)

(ii) [-3, 3]

(iii)  x is negative 

(iv) x is greater than or equal to 2 and less than or equal to 6.

Solution :

(i) (-∞, 7) ==> -∞< x < 7

(ii) [-3, 3] ==> -3 ≤ x ≤ 3

(iii)  x is negative ==>  x < 0

(iv) x is greater than or equal to 2 and less than or equal to 6.

x ≥ 2 and x ≤ 6

Problem 4 :

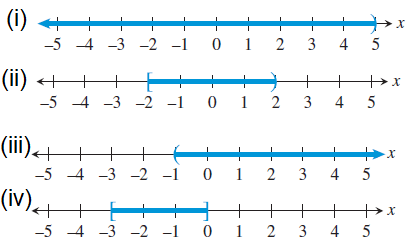
Solution :

(i) (-∞, 5)

(ii)  [-2, 2)

(iii)  (-1,∞)

(iv) [-3, 0] 

Problem 5 :

Convert to inequality notation. Find the endpoints and state whether the interval is bounded or unbounded and its type.

(i) (-3, 4]

(ii)  (-3, -1)

(iii)  (-∞, 5)

(iv)  [-6, ∞)

Solution :

(i) (-3, 4]

Inequality notation :

-3 < x  ≤ 4

Endpoints :

-3 and 4 are endpoints.

Bounded : Half open

(ii)  (-3, -1)

Inequality notation :

-3 < x < -1

Endpoints :

-3 and -1 are endpoints.

Bounded: Open

(iii)  (-∞, 5)

Inequality notation :

x < 5

Endpoints :

End point is 5.

Unbounded : Open

(iv)  [-6, ∞)

Inequality notation :

-6 < x < ∞

Endpoints :

Endpoint is -6

Unbounded : Half open