BEARING WORD PROBLEMS INVOLVING COSINE LAW

Problem 1 :

Two ships leave a harbor at the same time. One ship travels on a bearing of S12°W at 14 miles per hour. The other ship travels on a bearing of N75°E at 10 miles per hour. How far apart will the ships be after three hours? Round to the nearest tenth of a mile.

Solution :

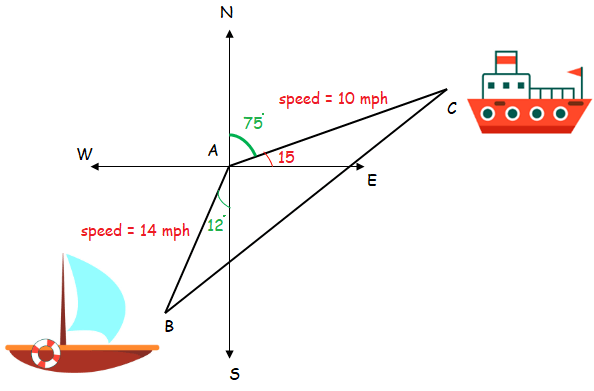
∠BAC = 12 + 90 + 15

= 117

Distance covered in between the positions A and B :

Distance = time x speed

= 3 x 14

AB = 42 miles 

Distance covered in between the positions A and C :

= 3 x 10

AC = 30 miles 

From this, we have to find distance between B and C.

So, the distance between two ships after 3 hours is 61.68 approximately 62 miles.

Problem 2 :

A plane leaves airport A and travels 580 miles to airport B on a bearing of N34°E. The plane later leaves airport B and travels to airport C 400 miles away on a bearing of S74°E. Find the distance from airport A to airport C to the nearest tenth of a mile.

Solution :

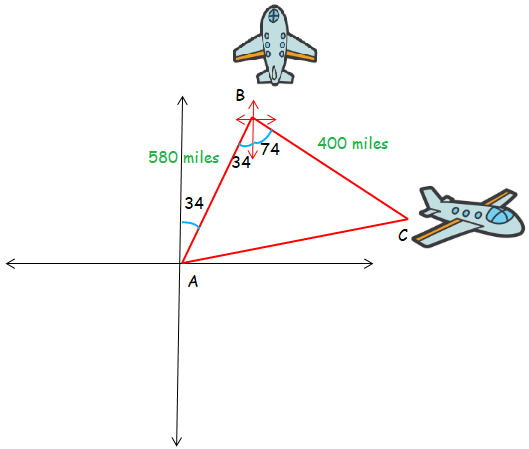
∠ABC = 34 + 74 ==> 108

Distance between airport A to C is 800 miles approximately.

Problem 3 :

You are on a fishing boat that leaves its pier and heads east. After traveling for 25 miles, there is a report warning of rough seas directly south. The captain turns the boat and follows a bearing of S40°W for 13.5 miles.

a. At this time, how far are you from the boat’s pier? Round to the nearest tenth of a mile.

b. What bearing could the boat have originally taken to arrive at this spot?

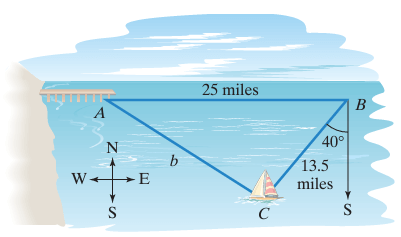
Solution :

a) Here we have to find the distance between AC :

AB = 25 miles, BC = 13.5 miles

∠ABC = 90 - 40

= 50

At this time, i am 19.3 miles away from the boat’s pier.

b)  To boat should take N40°W to reach the spot.

Problem 4 :

You are on a fishing boat that leaves its pier and heads east. After traveling for 30 miles, there is a report warning of rough seas directly south. The captain turns the boat and follows a bearing of S45°W for 12 miles.

a. At this time, how far are you from the boat’s pier? Round to the nearest tenth of a mile.

b. What bearing could the boat have originally taken to arrive at this spot?

Solution :

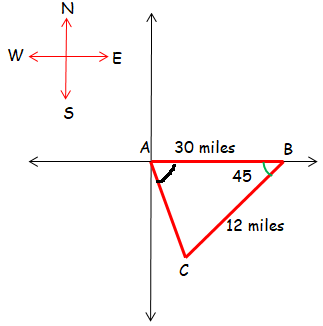
AB = 30 miles, BC = 12 miles

∠ABC = 45

a) From boat pier, i will be there are 23.13 miles distance.

b) To find the missing angle CAB, we can use sin law.

BC/sin A = AC/sin B = AB/sin C

12/sin A = 23.1/sin 45

12/sin A = 23/(√2/2)

12/sin A = 46/√2

sin A = 12(√2)/46

sin A = 0.369

A = sin^-1(0.369)

A = 21.6

Originally, he should take = 21.6 + 90

= 111.6

Problem 5 :

Two airplanes leave an airport at the same time on different runways. One flies on a bearing of N66°W at 325 miles per hour. The other airplane flies on a bearing of S26°W at 300 miles per hour. How far apart will the airplanes be after two hours?

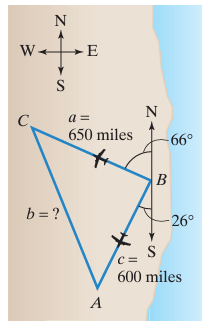
Solution :

∠ABC = 180 - 66 - 26

= 88

After two hours, the planes are approximately 869 miles apart.