BEARING AND TRIGONOMETRY WORD PROBLEMS WORKSHEET

Problem 1 :

The angle of depression from a kookaburra’s feet to a worm on a ground is 40°.The worm is 15 meters from a point on the ground directly below the kookaburra's feet.

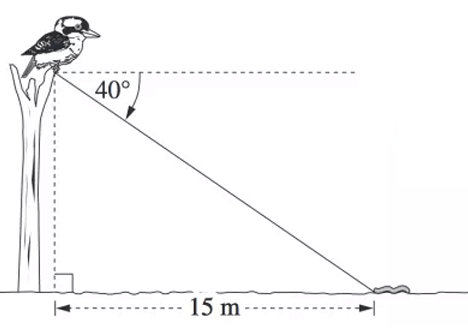
How high above the ground are the kookaburra's feet, correct to the nearest meter?

Solution

Problem 2 :

Danni is flying a kite that is attached to a string of length 80 meters. The string an angle of 55° with the horizontal. How high, to the nearest meter, is the kite above Danni's hand ?

Solution

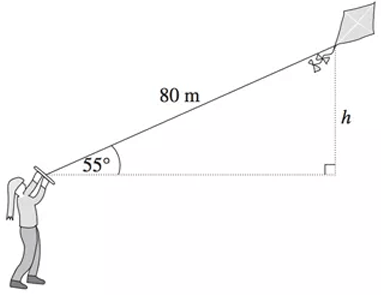
Problem 3 :

The plane flies on a bearing of 150° from A to B.

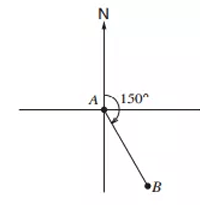
What is the bearing of A from B ?

Solution

Problem 4 :

Two trees on a ground level, 12 m apart are joined by a cable. It is attached 2 meters above the ground on one tree and 11 meters above the ground to the other.

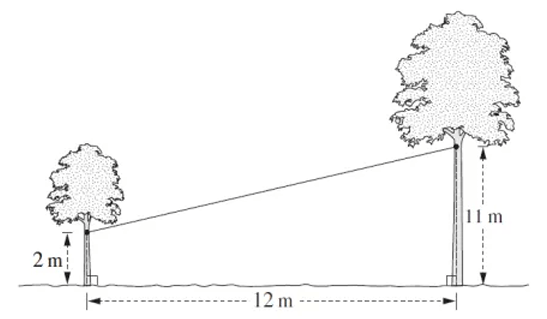
What is the length of the cable between the two trees ?

Solution

Problem 5 :

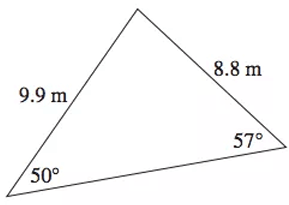
What is the area of the triangle ?

Solution

Problem 6 :

Three towns P, Q and R are marked to the diagram. The distance from R to P is 76 km. ∠RQP = 26° and ∠RPQ = 46°

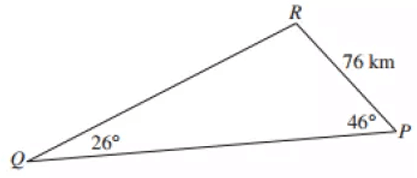
What is the distance between P to Q to the nearest km ?

Solution

Problem 7 :

Town B is 80 km due north of Town A and 59 km from Town C. Town A is 31 km from Town C.

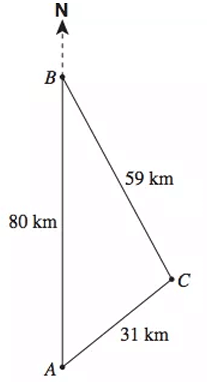
What is the bearing of Town C from Town B ?

Solution

Problem 8 :

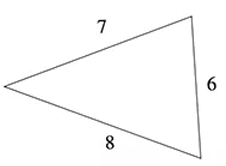
What is the size of the smallest angle in the triangle ?

Solution