BASIC GEOMETRY WORD PROBLEMS

Problem 1 :

Two sides of a triangle are 7 and 13 centimeters. The perimeter of is 27 cm. Find the third side.

Solution :

Let a, b and c be the sides of the triangle.

a = 7, b = 13

Perimeter = Sum of all the sides

a + b + c = 27

7 + 13 + c = 27

20 + c = 27

c = 27 - 20

c = 7 cm

Problem 2 :

Find the area of the triangle given below.

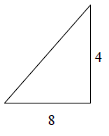
Solution :

Base = 8 and height = 4

Area of the triangle = (1/2) x base x height

= (1/2) x 8 x 4

= 16 cm²

Problem 3 :

If a square has an area of 49 ft², what is the length of one of its sides? The perimeter ?

Solution :

Area of the square = 49 ft²

a² = 49

a² = 7²

a = 7

Length of one sides of the triangle is 7 cm.

Perimeter = 4a

= 4 (7)

= 28 cm

Problem 4 :

If a rectangle has a width of 4, how long must its length be so that the area is 36 ?

Solution :

Width of the rectangle = 4

Let l be the length of the rectangle.

Area of the rectangle = length x width

36 = 4 x l

l = 36/4

l = 9

Problem 5 :

If one angle of a right triangle is 70 degree. What are the other 2 angles ?

Solution :

Since it is a right triangle, one of the angle should be 90 degree. Let x be the third angle measure.

Sum of interior angles of the triangle = 180

70 + 90 + x = 180

160 + x = 180

x = 180 - 160

x = 20

Problem 6 :

Find b.

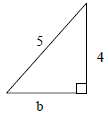
Solution :

Since it is right triangle, it holds the Pythagorean theorem.

5² = 4² + b²

25 = 16 + b²

25 - 16 = b²

b² = 9

b = 3

Problem 7 :

What is the diameter of the circle with an area of 16π ?

Solution :

Area of the circle = 16π

πr² = 16π

r² = 16

r = 4

d = 2(radius)

d = 2(4)

d = 8

So, the diameter of the circle is 8.

Problem 8 :

What is the circumference of the circle having an area of 25π (allow π = 3.14)

Solution :

Area of the circle = 25π

πr² = 25π

r² = 25

r = 5

Circumference of the circle = πd

= π(10)

= 20π

Problem 9 :

If the box has a height of 4 in, a length of 12 in and volume of 240 in³, what is the box's width.

Solution :

Height of the box = 4 inches, length = 12 inches

Let w be the width if the box.

Volume of the box = 240 in³

Volume of cuboid = length x width x height

4 x w x 12 = 240

w = 240/(4 x 12)

w = 5 inches

Problem 10 :

Find the volume of cylinder whose radius and height are 2 and 7 respectively.

Solution :

Volume of cylinder = πr²h

Radius = 2 and height = 7

Volume = (22/7) x 2² x 7

=  88

Problem 11 :

You cut a wooden block to make a CO2 racecar. The top right angle of the block is 105°. What is the measure of the top left angle?

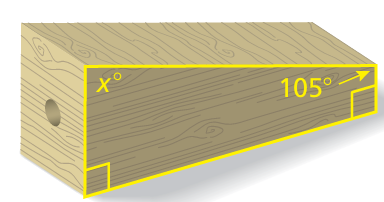
Solution :

In a quadrilateral, the sum of interior angles = 360

x + 90 + 90 + 105 = 360

x + 285 = 360

x = 360 - 285

x = 75

Problem 12 :

Copy and complete using always, sometimes, or never.

a)  A square is _____ a rectangle.

b)  A square is ______ a rhombus.

c)  A rhombus is  ______ a square.

d)  A parallelogram is ________ a trapezoid.

e) A trapezoid is _______ a kite.

f)  A rhombus is _______ a rectangle

Solution :

a)  A square is _____ a rectangle.

If all sides are equal, then the particular shape is a square, if opposite sides are equal then that shape is a rectangle.

Since all sides are equal, its opposite sides will also be equal. Then the square is always a rectangle. But the rectangle never will become a square.

b)  A square is ______ a rhombus.

If square all four sides will be equal and corner angles will become 90 degree, but in rhombus only four sides will be equal. Then square is always rhombus.

c)  A rhombus is sometimes a square.

d)  In parallelogram opposite side will be parallel and equal. The trapezoid will always two parallel and two non parallel sides.

A parallelogram is never a trapezoid.

e) A trapezoid is sometimes a kite.

f)  A rhombus is sometimes a rectangle

Problem 12 :

What is the area of the shaded figure shown below?

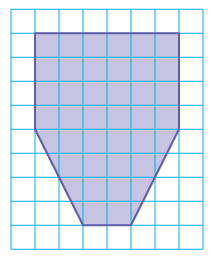
a) 32 units²      b)  40 units²          c) 44 units²        d) 56 units²

Solution :

The top is in the shape of rectangle, the bottom is in the shape of trapezoid.

Length = 4 units, width = 5 units

Length of parallel sides are 5 units and 2 units. Height = 4 units

Aeea of the shape = Area of rectangle + Area of trapezoid

= 4 x 5 + (1/2) x 4 (5 + 2)

= 20 + 2(7)

= 20 + 14

= 34 square units