AXIS OF SYMMETRY OF ABSOLUTE VALUE FUNCTION

What is axis of symmetry of absolute value function ?

The axis of symmetry  the line that divides the graph into two congruent halves.

Find equation of axis of symmetry of the following absolute value function.

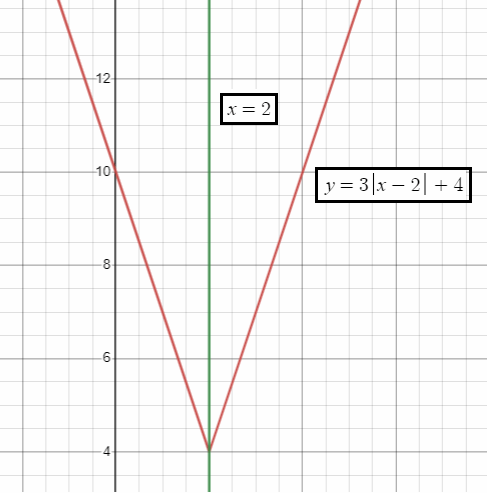
Problem 1 :

y = 3|x - 2| + 4

Solution :

y = 3|x - 2| + 4

y = a|x - h| + k

Vertex :

(h, k) = (2, 4)

Opens up/down :

Opens up

Value of a :

a = 3

Axis of symmetry :

Equation of axis of symmetry is at x = 2

Find equation of axis of symmetry of the following absolute value function.

Problem 2 :

y = -1/3|x + 1| + 4

Solution :

y = -1/3|x + 1| + 4

y = a|x - h| + k

Vertex :

(h, k) = (-1, 4)

Opens up/down :

Opens down

Value of a :

a = -1/3

Axis of symmetry :

Equation of axis of symmetry is at x = -1

Problem 3 :

y = 1/2|x + 3| - 2

Solution :

y = 1/2|x + 3| - 2

y = a|x - h| + k

Vertex :

(h, k) = (-3, -2)

Opens up/down :

Opens up

Value of a :

a = 1/2

Axis of symmetry :

Equation of axis of symmetry is at x = -3

Problem 4 :

y = -|x| + 3

Solution :

y = -|x - 0| + 3

y = a|x - h| + k

Vertex:

(h, k) = (0, 3)

Opens up/down :

Opens down

Value of a :

a = -1

Axis of symmetry :

Equation of axis of symmetry is at x = 0

Problem 5 :

y = -|2x|

Solution :

y = -|2x - 0| + 0

y = a|x - h| + k

Vertex :

(h, k) = (0, 0)

Opens up/down :

Opens down

Value of a :

a = -1

Axis of symmetry :

Equation of axis of symmetry is at x = 0

Problem 6 :

y = |-(x + 2)|

Solution :

y = |-x - 2| + 0

y = a|x - h| + k

Vertex :

(h, k) = (2, 0)

Opens up/down :

Opens up

Value of a :

a = 1

Axis of symmetry :

Equation of axis of symmetry is at x = 2