AREA OF TRIANGLES COMPOSITE SHAPES

Problem 1 :

Shown is a square garden with a triangular pond. Find the area of the garden that is grass.

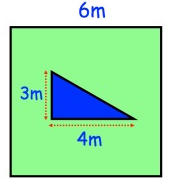
Solution :

area of square = a²

a = 6m

area of square = (6)²

area of square = 36m²

area of triangle = 1/2 × b × h

Base (b) = 4m 

Height (h) = 3m

area of triangle = 1/2 × 4 × 3

= 12/2

= 6m²

 The area of the garden that is grass = 36 - 6

= 30m²

So, the area of the garden that is grass is 30m².

Problem 2 :

Shown is a triangular brick wall with a rectangular window. Find the area of the wall that is brick.

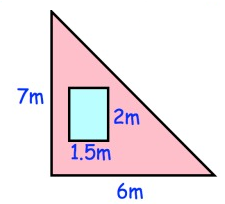
Solution :

area of rectangle = l × w

Length = 1.5m

Width = 2m

area of rectangle = 1.5 × 2

area of rectangle = 3m²

area of triangle = 1/2 × b × h

Base (b) = 6m 

Height (h) = 7m

area of triangle = 1/2 × 6 × 7

= 42/2

area of triangle = 21m²

area of the wall = area of triangle - area of rectangle

= 21m² - 3m²

area of the wall = 18m²

Problem 3 :

Shown is a pattern that is made from a rectangle and a triangle. Find the area of the pattern.

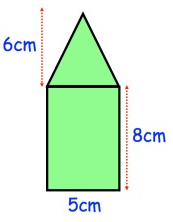
Solution :

area of rectangle = l × w

Length = 5cm

Width = 8cm

area of rectangle = 5 × 8

area of rectangle = 40 cm²

area of triangle = 1/2 × b × h

Base (b) = 5 cm 

Height (h) = 6 m

area of triangle = 1/2 × 5 × 6

= 30/2

area of triangle = 15cm²

area of the pattern = area of rectangle + area of triangle - 

= 40 cm² + 15 cm²

area of the pattern = 55cm²

Problem 4 :

Shown below is a wall. Calculate the area of the wall.

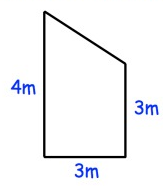
Solution :

Area of trapezoid = 1/2 (a + b) × h

= 1/2 (3 + 4) × 3

= 1/2 × 7 × 3

= 21/2

= 10.5

So, area of the wall is 10.5m².

Problem 5 :

Shown below is a logo made from a square and two triangles. Calculate the area of the logo.

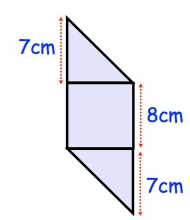
Solution :

area of square = a²

a = 8cm

area of square = (8)²

area of square = 64cm²

area of triangle = 1/2 × b × h

Base (b) = 8cm 

Height (h) = 7cm

area of triangle = 1/2 × 8 × 7

= 56/2

= 28cm²

area of triangle = 1/2 × b × h

Base (b) = 8cm 

Height (h) = 7cm

area of triangle = 1/2 × 8 × 7

= 56/2

= 28cm²

area of the logo = area of square + 2(area of rectangle)

= 64 + 2(28)

= 64 + 56

= 120

So, area of the logo is 120 cm².

Problem 6 :

Below is a diagram of a right-angled triangle and a square.

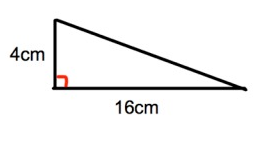The area of the square is twice the area of the triangle.

Calculate the length of each side of the square.

Solution :

area of triangle = 1/2 × b × h

Base (b) = 16cm 

Height (h) = 4cm

area of triangle = 1/2 × 16 × 4

= 64/2

area of triangle = 32cm²

The area of the square is twice the area of the triangle.

So, area of the square is 2 × 32

= 64 cm²

area of square = a²

64 = a²

a = √64

a = 8

So, the length of each side of the square is 8 cm.

Problem 7 :

The area of the triangle is 165cm², find b.

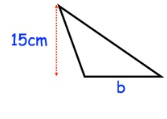
Solution :

area of triangle = 1/2 (b × h)

base = b

height = 15 cm

165 = 1/2 × b × 15

165 = 15/2 × b

(165 × 2)/15 = b

330/15 = b

b = 22

Problem 8 :

Shown below is a right-angled triangle.

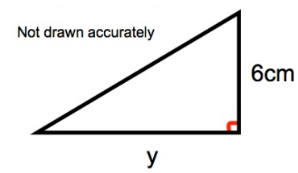
The area of the triangle is 21cm². Calculate y, the length of the base.

Solution :

area of triangle = 1/2 (b × h)

base = y

height = 6 cm

21 = 1/2 × b × 6

21 = 6/2 × b

(21 × 2)/6 = b

42/6 = b

b = 7

Hence y the length of the base is 7 cm.

Problem 7 :

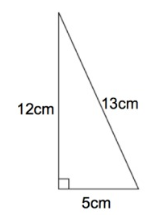
Below is a right-angled triangle and a rectangle.

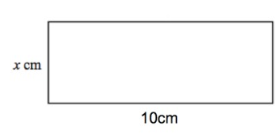The area of the right-angled triangle is equal to the area of the rectangle. calculate x.

Solution :

area of triangle = 1/2 × b × h

Base (b) = 5 cm 

Height (h) = 12 cm

area of triangle = 1/2 × 5 × 12

= 60/2

= 30

area of rectangle = l × w

Length = 10 cm

Width = x cm

area of rectangle = 10 × x

Area of the right-angled triangle is equal to the area of the rectangle.

30 = 10x

x = 30/10

x = 3 cm