AREA OF TRIANGLE WITH COORDINATES

Problem 1 :

Find the area of the triangle ABC with A(1, -4) and the mid-points of sides through A being (2, -1) and (0, -1).

Solution :

The coordinates of the mid point of the line segment joining the points P(x₁, y₁) and Q(x₂, y₂) are

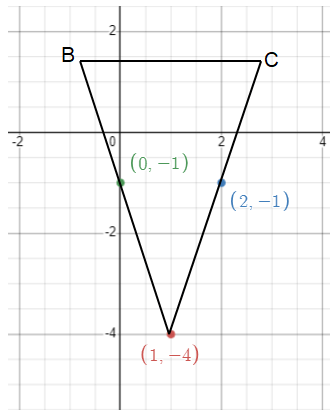
Given, the midpoint A(1, -4) and (x, y) is (2, -1)

The coordinates of B is (3, 2).

Given, the midpoint of A(1, -4) and C(a, b) is (0, -1).

The coordinates of C are (-1, 2).

The area of a triangle with vertices A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃)

The area of a triangle with vertices A(1, -4), B(3, 2) and C(-1, 2)

Therefore, the area of the triangle ABC is 12 square units.

Problem 2 :

Find the value of m if the points (5, 1), (-2, -3) and (8, 2m) are collinear.

Solution:

Points A, B, C will be collinear if the area of ΔABC = 0

Hence, the required value of m = 19/14.

Problem 3 :

Find the area of the triangle whose vertices are (-8, 4), (-6, 6) and (-3, 9)

Solution:

Let the vertices of triangle be,

A(x₁, y₁) = (-8, 4)  B(x₂, y₂) = (-6, 6) and C(x₃, y₃) = (-3, 9)

Hence, area of the triangle with vertices (-8, 4), (-6, 6) and (-3, 9) is 0 square units.

Problem 4 :

The points A(2, 9), B(a, 5) and C(5, 5) are the vertices of a triangle ABC right angles at B. Find the values of a and hence the area of ΔABC.

Solution:

Given, the points A(2, 9), B(a, 5) and C(5, 5) are the vertices of right angle triangle whose angle B is right angle.

By distance formula,

AB² + BC² = CA²

Put first a = 2, In AB, BC and CA

Then,

Now, put a = 5 and we get,

Then a = 5 is not possible.

Hence a = 2 is possible for all value of right angle triangle.

Area of the right angles triangle ABC is

Problem 4 :

A(6, 1), B(8, 2) and C(9, 4) are three vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of ΔADE.

Solution:

Let fourth vertex of ABCD be D(x, y). We know that, the diagonals of a parallelogram bisects each other.

Mid point of BD = Mid point of AC

Thus, the required fourth vertex D is (7, 3).

Now, midpoint of DC 

Area of ΔADE with vertices A(6, 1), D(7, 3) and E(8,7/2) is 

Hence, the area of  ΔADE is 3/4 square units.