AREA OF TRIANGLE USING HERONS FORMULA

Problem 1 :

Find the area of the triangle with a = 12 yards, b = 16 yards and c = 24 yards. Round to the nearest square yard.

Solution :

Finding half of the perimeter :

Finding area :

Area of the triangles is approximately 85 square yards.

Problem 2 :

Find the area of the triangle with a = 4 feet, b = 4 feet and c = 2 feet. Round to the nearest square yard.

Solution :

Finding half of the perimeter :

Finding area :

Area of the triangles is approximately 4 square feet.

Problem 3 :

The sides of a triangular field are 41 m, 40 m and 9 m. Find the number of rose beds that can be prepared in the field, if each rose bed, on an average needs 900 cm² space.

Solution :

a = 41 m, b = 40 m and c = 9 m

Finding semi perimeter :

Finding area :

Area of the field = 180 square meter.

Each rose bed can occupy 900 cm² space.

Converting in m², 

900 cm² = 900/10000

= 0.09 m²

Number of rose beds can be prepared = 180/0.09

= 2000 rose beds.

Problem 4 :

Calculate the area of the shaded region given below.

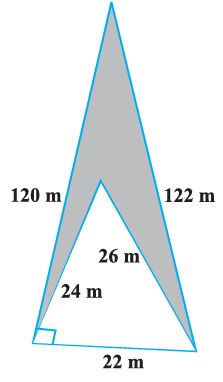
Solution :

Area of the shaped region

= (area of triangles whose sides are 120 m, 122 m and 22 m)

- 

(area of triangles whose sides are 22 m, 24 m and 26 m)

Area of large triangle :

Area of small triangle :

= 1320 - 246

Area of the shaded region = 1074 square meter.

Problem 5 :

Find the cost of laying grass in a triangular field of sides 50 m, 65 m and 65 m at the rate of $7 per m².

Solution :

Area of triangular field :

Cost of laying grass in the triangular field = 7 x 900

= $6300

Problem 6 :

The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 13 m, 14 m and 15 m. The advertisements yield an earning of $200 per m² a year. A company hired one of its walls for 6 months. How much rent did it pay?

Solution :

Area of the wall in which advertisement to be placed 

= √s(s-a)(s-b)(s-c)

s = (a + b + c)/2

a = 13 m, b = 14 m and c = 15 m

s = (13 + 14 + 15)/2

= 42/2

s = 21

Area = √21(21-13)(21-14)(21-15)

= √21 x 8 x 7 x 6

= √7056

= 84 m²

Cost of advertisement per month = 200/12

= 16.66 per month per m²

Rent for 6 month for 84 m² = 16.66 x 84

= $1394.54

Problem 7 :

Find the semi perimeter of a triangle having the length of its sides as 20 cm,15 cm and 9 cm.

Solution :

Semi perimeter o the scalene triangle = s

s = (a + b + c)/2

Here a = 20 cm, b = 15 cm and c = 9 cm

s = (20 + 15 + 9) / 2

= 44/2

= 22 cm

Problem 8 :

The edges of a triangular board are 6 cm, 8 cm and 10 cm. Find the cost of painting it at `0.09 per cm²

Solution :

s = (a + b + c)/2

Here a = 6 cm, b = 8 cm and c = 10 cm

s = (6 + 8 + 10) / 2

= 24/2

= 12 cm

Area = √12(12-6)(12-8)(12-10)

= √12 x 6 x 4 x 2

= √576

= 24 cm²

Cost of painting = 0.09

Required cost = 0.09 x 24

= $2.16

Problem 9 :

The perimeter of a triangle is 54 cm and its sides are in the ratio 5:6:7. Find the area of the triangle.

Solution :

Perimeter of the triangle = 54 cm

From the given ratio, side lengths of the triangle are 5x, 6x and 7x

5x + 6x + 7x = 54

18x = 54

x = 3

Side lengths are 5(3), 6(3) and 7(3)

that is,

 15 cm, 18 cm and 21 cm

s = (15 + 18 + 21) / 2

= 54/2

= 27 cm

Area = √27(27-15)(27-18)(27-21)

= √27 x 12 x 9 x 6

= √17496

= 132.27 cm²

Problem 10 :

Find the perimeter of an equilateral triangle whose area is equal to that of a triangle with sides 21 cm, 16 cm and 13 cm.

Solution :

Let us find the area of triangle whose side lengths are 21 cm, 16 cm and 13 cm.

a = 21 cm, b = 16 cm and c = 13 cm

s = (21 + 16 + 13) / 2

= 50/2

= 25 cm

Area = √25(25-21)(25-16)(25-13)

= √25 x 4 x 9 x 12

= √10800

= 103.92 cm²

Approximately = 104 cm²

Area of equilateral triangle = 104 cm²

(√3/4) a² = 104

a² = 104 (4/√3)

a² = 104 (4/√3)

a² = 240.18

a = 15.49

So, the required side length is 15.49 cm.