HOW TO FIND THE AREA OF A TRIANGLE USING SINE LAW

Problem 1 :

Find the area of:

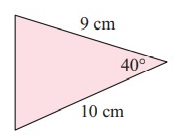
Solution:

Given, ∠A = 40˚, b = 9 cm, c = 10 cm

Area of triangle = 1/2 × b × c × sin A

= 1/2 × 9 × 10 × sin 40˚

= 1/2 × 9 × 10 × 0.64

A = 28.9 cm²

Problem 2 :

Find the area of the triangle given below.

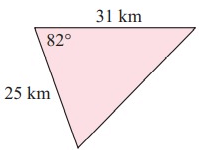
Solution:

Given, ∠A = 82˚, b = 25 km, c = 31 km

Area of triangle = 1/2 × b × c × sin A

= 1/2 × 25 × 31 × sin 82˚

= 1/2 × 25 × 31` × 0.99

 = 383.625 km²

A = 384 km²

Problem 3 :

Find the area of the triangle given below.

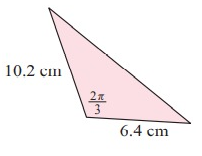
Solution:

Given, ∠A = 2π/3, b = 10.2 cm, c = 6.4 cm

Area of triangle = 1/2 × b × c × sin A

= 1/2 × 10.2 × 6.4 × sin 2π/3

= 1/2 × 10.2 × 6.4` × √3/2

 = 28.26 cm²

A = 28.3 cm²

Problem 2 :

If triangle ABC has area 150 cm², find the value of x:

Solution:

Area of triangle = 1/2 × a × c × sin B

150 = 1/2 × 17 × x × sin 68˚

300 = 17x × 0.927

17x = 300/0.927

17x = 323.6

x = 323.6/17

x = 19.0

So, the value of x is 19.0.

Problem 3 :

A parallelogram has two adjacent sides of length 4 cm and 6 cm respectively. If the included angle measures 52˚, find the area of the parallelogram.

Solution:

Given, x = 4 cm and y = 6 cm

Area of Rhombus = xy sin θ

= 4 × 6 × sin 52˚

= 24 × 0.78

= 18.91 cm²

So, area of parallelogram is 18.9 cm².

Problem 4 :

A rhombus has sides of length 12 cm and an angle 72˚. Find its area.

Solution:

Given, side length = 12 cm, θ = 72˚

Area of Rhombus = a² sin θ

= (12)² sin (72˚)

= 144  × 0.95

= 136.95 cm²

So, area of rhombus is 137 cm². 

Problem 5 :

Find the area of a regular hexagon with sides of length 12 cm.

Solution:

Given, side length = 12 cm

Area of regular hexagon = 3/2 (√3) a²

=  3/2 (√3) (12)²

= 3/2 (√3) (144)

= 216 × 1.732

= 374.112

So, area of regular hexagon is 374 cm².

Problem 6 :

A rhombus has an area of 50 cm² and an internal angle of size 63˚. Find the length of its sides.

Solution:

Given, Area of rhombus = 50cm²

Internal angle θ = 63˚

Area of Rhombus = a² sin θ

50 =  a² sin  63˚

a² = 50/sin 63˚

a² = 50/0.89

a² = 56.17

a = 7.49 cm

So, side length of the rhombus is 7.49 cm.

Problem 7 :

A regular pentagonal garden plot has centre of symmetry O and an area of 338 m². Find the distance OA.

Solution:

Area of each triangular sector = 338/5

Angle subtended at centre = 360/5 = 72˚

Let circum radius of pentagon = r

Side of pentagon = 2rsin 36˚

Apothem = rcos 36˚

Area of each sector = 1/2 (2r sin 36˚) (r cos 36˚)

= r²/2sin 72˚ = 338/5

r² = 338/5 × 2/sin 72˚

r² = 142.16

r = 11.9 m

Find the possible values of the included angle of a triangle with:

Problem 8 :

Sides 5 cm and 8 cm and area 15 cm²

Solution:

Area of triangle = 1/2 × a × b × sin θ

15 = 1/2 × 5 × 8 × sin θ

30 = 40 × sin θ

sin θ = 30/40

sin θ = 0.75

θ = sin^-1 (0.75)

θ = 48.6˚

Problem 9 :

Sides 45 km and 53 km and area 800 km²

Solution :

Area of triangle = 1/2 × a × b × sin θ

800 = 1/2 × 45 × 53 × sin θ

1600 = 2385 × sin θ

sin θ = 1600/2385

sin θ = 0.67

θ = sin^-1 (0.67)

θ = 42.1