AREA OF SECTOR WITH RADIUS AND ARC LENGTH

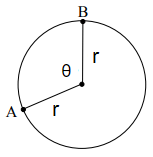
Length of arc = (θ/360) x 2πr

Problem 1 :

A circle has an arc whose measure is 18° and whose length is 88π . Find

i) Radius     ii)  area of sector

Solution :

Arc measure = 18°

Length of arc = 88π

(θ/360) x 2πr = 88π

(18/360) x 2πr = 88π

r = 88/10

r = 8.8

Area of sector = (18/360) x π(8.8)²

= 12.15

Problem 2 :

A circle has a circumference whose length is 25π . Find the area of sector whose central angle is 90°

Solution :

Arc measure = 90°

Length of arc = 25π

(θ/360) x 2πr = 25π

(90/360) x 2πr = 25π

r = 50

Area of sector = (90/360) x π(50)²

= 625π

Problem 3 :

Find the measure of the central angle of an arc if its length is 14π and the radius is 18. Find the area of sector.

Solution :

radius = 18

Length of arc = 14π

(θ/360) x 2πr = 14π

(θ/360) x 2π x 18 = 14π

θ = 140

Area of sector = (θ/360) x πr²

= (140/360) x π(18)²

= 395.64

Find the area of sector RST in ⊙ S using the given information. Leave your answer in terms of π.

Problem 4 :

r = 3 in, mRT = 30

Solution:

Formula for area of a sector is given by

Substitute m∠RT = 30 and r = 3

Problem 5 :

r = 8 mm, mRT = 90

Solution:

Substitute m∠RT = 90 and r = 8

Problem 6 :

d = 10 ft, mTR = 180

Solution:

Formula for area of a sector is given by

Substitute m∠TR = 180 and d = 10

r = 10/2

r = 5

Problem 7 :

d = 13 m, mTR = 120

Solution:

Formula for area of a sector is given by

Substitute m∠TR = 120 and d = 13

r = 13/2

r = 6.5