AREA OF SECTOR WHEN ANGLE IS GIVEN AS RADIAN

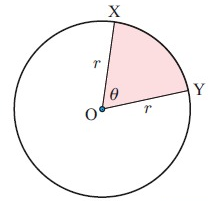
In the diagram, the area of minor sector XOY is shaded. θ is measured in radians. We use a ratio to obtain :

area of sector/area of circle = θ/2π

A/πr² =  θ/2π

A = (1/2)θr²

For θ in radians, area of sector A = (1/2)θr²

For θ in degrees, area of sector A = (θ/360) × πr²

Problem 1 :

Use radians to find the arc length and area of a sector of a circle of :

a. radius 9 cm and angle 7π/4

b. radius 4.93 cm and angle 4.67 radians.

Solution :

a) radius r = 9 cm

angle θ = 7π/4

arc length = rθ

= 9 × 7π/4

= 9 × 7(3.14)/4

= 197.82/4

= 49.455 cm

Area of sector = 1/2(θr²)

= 1/2 × 7π/4 × (9)²

= 1/2 × 7(3.14)/4 × 81

= 1780.38/8

= 222.55 cm²

b)  radius r = 4.93 cm

angle θ = 4.67

arc length = rθ

= 4.93 × 4.67

= 23.02 cm

Area of sector = 1/2(θr²)

= 1/2 × 4.67× (4.93)²

= 1/2 × 4.67 × 24.30

= 56.74 cm²

Problem 2 :

A sector has an angle of 1.19 radians and an area of 20.8 cm². Find its :

a. radius  b. perimeter

Solution :

a.

Angle θ =  1.19

Area A = 20.8 cm²

area of sector A = (1/2)θr²

20.8 = (1/2) × 1.19 × r²

20.8 = 0.595 × r²

r² = 20.8/0.595

r² = 34.9580

 r = 5.91 cm

b.

P = 2r + l 

l = θr

l = 1.19 × 5.91

l = 7.03

P = 2(5.91) + 7.03

P = 11.82 + 7.03

p = 18.9 cm

Problem 3 :

Find, in radians, the angle of a sector of :

a. radius 4.3 m and arc length 2.95 m

b. radius 10 cm and area 30 cm²

Solution :

a.

 radius r = 4.3 m 

arc length l = 2.95 m

Using arc length formula,

l = θr

2.95 = θ × 4.3

θ = 2.95/4.3

θ = 0.686

So, the angle of a sector measures is 0.686 m.

b.

Given, radius r = 10 cm

area A = 30 cm²

area of sector A = (1/2)θr²

30 = (1/2) × θ × (10)²

30 = (1/2) × θ × 100

30 = 50 × θ

θ = 30/50

θ = 0.6

So, the angle of the sector measures is 0.6 cm².

Problem 4 :

Find θ (in radians ) for each of the following, and hence find the area of each figure :

a.          

b.

c.

Solution :

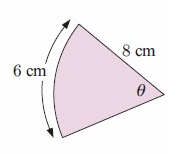
a. By observing the figure, 

radius r = 8 cm

area of sector s = 6 cm

s = rθ

6 = 8 × θ

6/8 = θ 

θ = 0.75 cm

area = 1/2 × θr²

= 1/2 × 0.75 × 8² 

= 1/2 × 0.75 × 64

area = 24 cm²

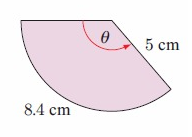
b. By observing the figure, 

radius r = 5 cm

area of sector s = 8.4 cm

s = rθ

8.4 = 5 × θ

8.4/5 = θ 

θ = 1.68 cm

area = 1/2 × θr²

= 1/2 × 1.68 × 5² 

= 1/2 × 1.68 × 25

area = 21 cm²

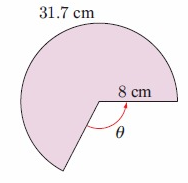
c. By observing the figure, 

radius r = 8 cm

area of sector s = 31.7 cm

s = rθ

31.7= 8 × θ

31.7/8 = θ 

θ = 3.9625 cm

area = 1/2 × θr²

= 1/2 × 3.9625 × 8² 

= 1/2 × 3.9625 × 64

area = 126.8cm²

Problem 5 :

Find the arc length and area of a sector of radius 5 cm and angle 2 radians.

Solution :

radius r = 5 cm

angle θ = 2 radians

l = θr

l = 2 × 5

l = 10 cm

So, arc length is 10 cm.

area of sector A = (1/2)θr²

= (1/2) × 2 × (5)²

= 25 cm²

So, area of a sector is 25 cm².