AREA OF COMPOUND SHAPES

Find the area of compound shapes given below.

Problem 1 :

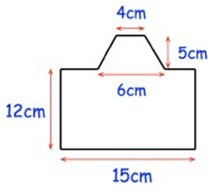
Solution :

Area of Compound Shapes = Area of rectangle + area of trapezoid

Problem 2 :

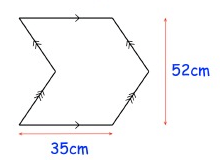
Solution :

By drawing the horizontal line in the middle, we get two parallelograms of same measures.

Area of parallelogram = base x height

height of one parallelogram = 26

= 2(35× 26)

= 3640

So, area of the shape is 3640 cm²

Problem 3 :

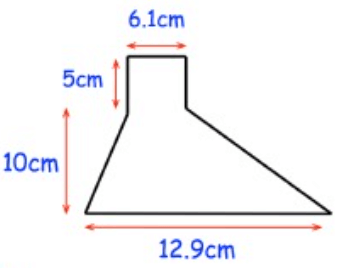
Solution :

By drawing the horizontal line in the middle, we divide the original shape into rectangle and trapezoid.

Problem 4 :

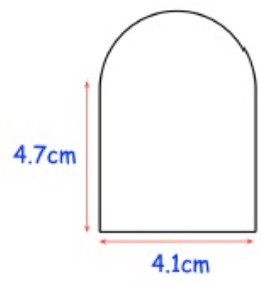
Solution :

Area of the shape 

= area of semi circle + area of rectangle

= (1/2) πr² + (l × w)

= (1/2) π(2.05)² + (4.1 × 4.7)

= (1/2) π(4.2025) + 19.27

= 2.10125π +19.27

= 2.10125(3.14) +19.27

= 6.60 + 19.27

= 25.87 cm²

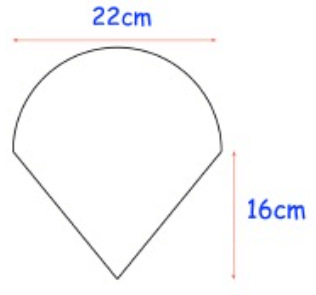
Problem 5 :

Solution :

Area of the shape = area of semi circle + area of triangle

= (1/2) πr² + (1/2) b × h

= (1/2) π(11)² + (1/2) x (22) × (16)

= (1/2) π(121) + 176

= π(60.5) + 176

= (3.14) × (60.5) + 176

= 189.97 + 176  

= 365.97 cm²

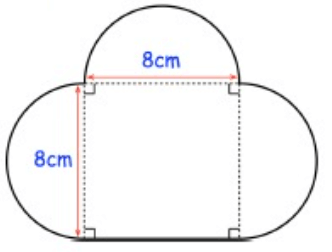
Problem 6 :

Solution :

Area of the shape

= 3(area of semi circle) + area of rectangle

= 3((1/2) πr²)) + (l × w)

= 1.5 x (3.14) × 4² + (8 × 8)

= 1.5 (3.14) × 16 + 64

= 75.36 + 64

= 139.36 cm²

Problem 7 :

Your family hires a company to install invisible fencing around your yard.

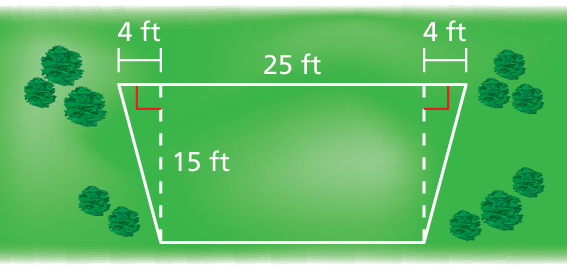
Part A : Find the area of the yard using only the area formulas for rectangles and triangles. Show your work.

Part B : Find the area of the yard using the area formula for trapezoids.

Part C : Explain why the two methods of finding the area of the yard give the same result. Describe the advantages of each method.

Solution :

Part A :

Area of triangle = 1/2 x base x height

base = 4 ft and height = 15 ft

Area of two triangles = 2 x 1/2 x 4 x 15

= 60 square feet

Area of rectangle = length x width 

= 25 x 15

= 375 square feet

Area of the shpae in total = 60 + 375

= 435 square feet

Part B :

Area of trapezoid = (1/2) x height x sum of length of parallel sides

= (1/2) x 15 x (25 + 25 + 8)

= (1/2) x 15 x 58

= 15 x 29

= 435 square feet

Part C :

The easiest way is using the formula of trapezoid, because using one formula we will find the area of the shape.

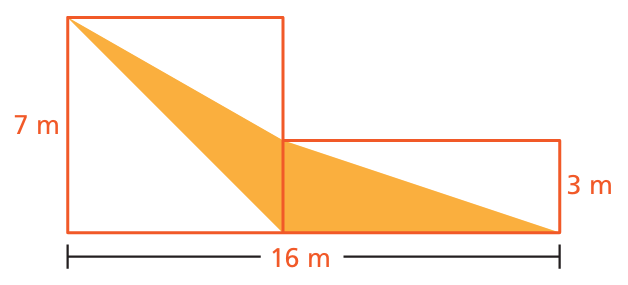
Problem 8 :

The figure is made up of a square and a rectangle. Find the area of the shaded region.

Solution :

Area of triangle shaded in the square :

Area of triangle shaded in the square = (1/2) x base x height

= (1/2) x 3 x 7

= 21/2

= 10.5 square meter

Area of triangle shaded in the rectangle :

Length of rectangle = 16 - 7

= 9 m

Width of rectangle = height of triangle = 3 m

Area of triangle in the rectangle = (1/2) x 3 x 9

= 27/2

= 13.5 square meter

Total area of shaded region = 9 + 13.5

= 22.5 square meter

Problem 9 :

The fountain is made up of two semicircles and a quarter circle. Find the perimeter and area of the fountain.

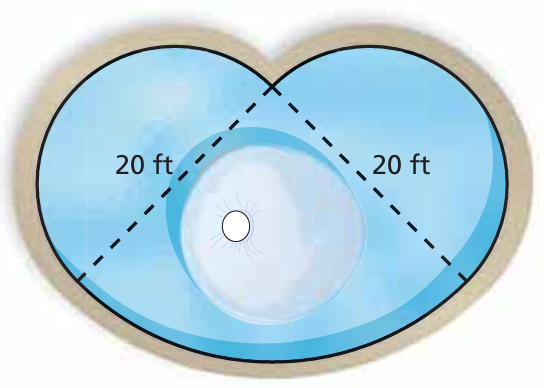
Solution :

Perimeter of semicircle (the arc alone in the figure shown) = πr 

Perimeter of quadrant (the arc alone in the figure shown) = πr/2

Perimeter of the shape = (πr + πr/2)

Diameter = 20 ft, radius = 10 ft

= π (10 + 10/2)

= 3.14(10 + 5)

= 3.14(15)

= 47.1 meter

Area of semicircle = (1/2) πr²

Area of quadrant = (1/4) πr²

Area of the shape shown = (1/2) πr² + (1/4) πr²

= (3/4) πr²

= (3/4) x 3.14 x 10²

= 0.75 x 3.14 x 100

= 235.5 square meter.

Find the area of the figure

Problem 10 :

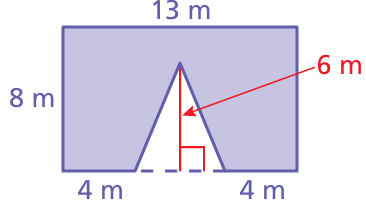
Solution :

Area of shaded region = area of rectangle - area of triangle

About rectangle :

Length = 13 m, width = 8 m

About triangle :

base = 13 - 8 ==> 5 m

Height = 6 m

= 8 x 13 - (1/2) x 5 x 6

= 104 - 15

= 89 square meter

Problem 11 :

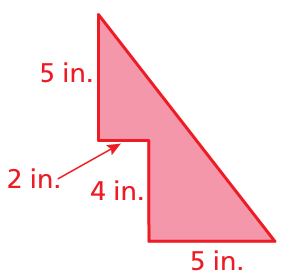
Solution :

Area of shaded regiuon = area of triangle - area of rectangle

About triangle :

base = 5 + 2 ==> 7 in

height = 5 + 4 ==> 9 in

About rectangle :

length = 2 in and width = 4 in

= (1/2) x 7 x 9 - 2 x 4

= 31.5 - 8

= 23.5 square inches

Problem 12 :

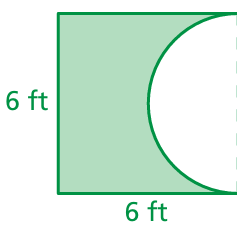
Solution :

Area of shaded region = Area of sqaure - area of semicircle

Side length of square = diameter of semicicle = 6 ft

radius = 3 ft

= 6² - (1/2)πr²

= 36 - 0.5 x 3.14 (3)²

= 36 - 14.13

= 21.87 square feet