AREA OF COMPOUND SHAPES RECTANGLES AND TRIANGLES

Find the area of the following compound shapes (not drawn to scale)

The dashed lines are perpendicular.

Problem 1 :

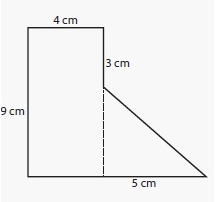
Solution :

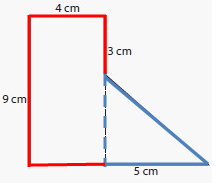
By observing the figure,

Area of a rectangle A = l × w

Length of a rectangle (l) = 4 cm

Width of a rectangle (w) = 9 cm

Area of a rectangle A = 4 × 9

= 36 cm²

Area of a triangle A = 1/2 (b × h)

Base of a triangle (b) = 5 cm

Height of a triangle (h) = 6 cm

= 1/2 (5 × 6)

= 1/2 (30)

= 15 cm²

Area of Compound Shapes = Area of a rectangle + Area of a triangle  

= 36 + 15

= 51 cm²

Problem 2 :

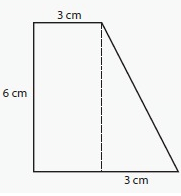
Solution :

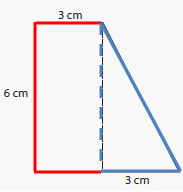
By observing the figure,

Area of a rectangle A = l × w

Length of a rectangle (l) = 3 cm

Width of a rectangle (w) = 6 cm

Area of a rectangle A = 3 × 6

= 18 cm²

Area of a triangle A = 1/2 (b × h)

Base of a triangle (b) = 3 cm

Height of a triangle (h) = 6 cm

= 1/2 (3 × 6)

= 1/2 (18)

= 9 cm²

Area of Compound Shapes = Area of a rectangle + Area of a triangle  

= 18 + 9

= 27 cm²

Problem 3 :

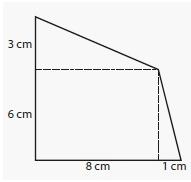
Solution :

By observing the figure,

Area of a rectangle A = l × w

Length of a rectangle (l) = 8 cm

Width of a rectangle (w) = 6 cm

Area of a rectangle A = 8 × 6

= 48 cm²

Area of a triangle A = 1/2 (b × h)

Base of a triangle (b) = 1 cm

Height of a triangle (h) = 6 cm

= 1/2 (1 × 6)

= 1/2 (6)

= 3 cm²

Area of a triangle A = 1/2 (b × h)

Base of a triangle (b) = 8 cm

Height of a triangle (h) = 3 cm

= 1/2 (8 × 3)

= 1/2 (24)

= 12 cm²

Area of Compound Shapes = Area of a rectangle + Area of a triangle + Area of a triangle  

= 48+ 3 + 12

= 63 cm²

Problem 4 :

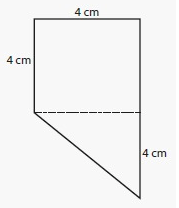
Solution :

By observing the figure,

Area of a rectangle A = l × w

Length of a rectangle (l) = 4 cm

Width of a rectangle (w) = 4 cm

Area of a rectangle A = 4 × 4

= 16 cm²

Area of a triangle A = 1/2 (b × h)

Base of a triangle (b) = 4 cm

Height of a triangle (h) = 4 cm

= 1/2 (4 × 4)

= 1/2 (16)

= 8 cm²

Area of Compound Shapes = Area of a rectangle + Area of a triangle  

= 16 + 8

= 24 cm²

Problem 5 :

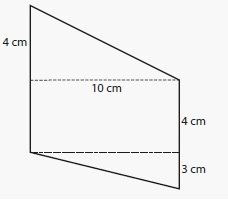
Solution :

By observing the figure,

Area of a rectangle A = l × w

Length of a rectangle (l) = 10 cm

Width of a rectangle (w) = 4 cm

Area of a rectangle A = 10 × 4

= 40 cm²

Area of a triangle A = 1/2 (b × h)

Base of a triangle (b) = 10 cm

Height of a triangle (h) = 3 cm

= 1/2 (10 × 3)

= 1/2 (30)

= 15 cm²

Area of a triangle A = 1/2 (b × h)

Base of a triangle (b) = 10 cm

Height of a triangle (h) = 4 cm

= 1/2 (10 × 4)

= 1/2 (40)

= 20 cm²

Area of Compound Shapes = Area of a rectangle + Area of a triangle + Area of a triangle  

= 40 + 15 + 20

= 75 cm²

Problem 6 :

Solution :

By observing the figure,

Area of a rectangle A = l × w

Length of a rectangle (l) = 10 cm

Width of a rectangle (w) = 4 cm

Area of a rectangle A = 10 × 4

= 40 cm²

Area of a triangle A = 1/2 (b × h)

Base of a triangle (b) = 7 cm

Height of a triangle (h) = 6 cm

= 1/2 (7 × 6)

= 1/2 (42)

= 21 cm²

Area of Compound Shapes = Area of a rectangle + Area of a triangle  

= 40 + 21

= 61 cm²

Problem 7 :

Find the area of the portion of the basketball court shown.

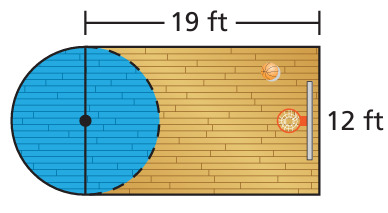
Solution :

The half of the circle is merged in the rectangle and finding out half of the circle is enough.

Area of portion of the basketbal = area of rectangle + (1/2) πr²

Length = 19 ft, width = 12 ft and diameter of circle = 12 ft, radius = 6 ft

= 12 x 19 + (1/2) x 3.14 x 6²

= 228 + 1.57 x 36

= 228 + 56.52

= 284.52 square ft.

Problem 8 :

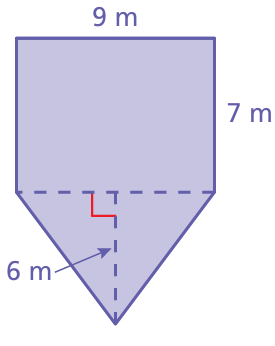
Solution :

Area of compound shape = area of triangle + area of rectangle

= (1/2) x base x height + length x width

= (1/2) x 9 x 6 + 7 x 9

= 27 + 63

= 100 square meter.

Problem 9 :

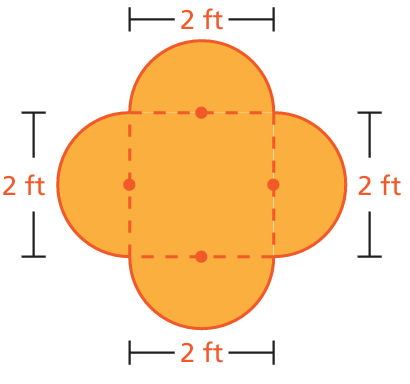
Solution :

Area of compound shape = area of square + 4 (area of semicircle)

= side x side + 4 x  (1/2) πr²

= 2 x 2 + 4 x (1/2) x 3.14 x 1²

= 4 + 6.28

= 10.58 square ft.

Problem 10 :

The figure is made up of a square and a rectangle. Find the area of the shaded region.

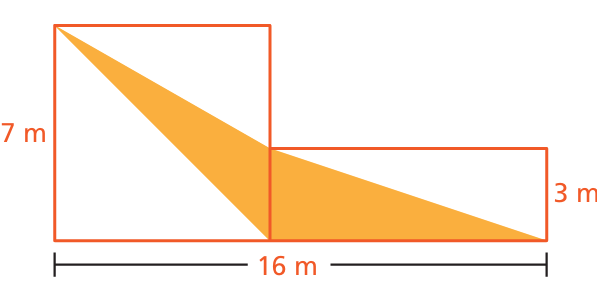
Solution :

base of the triangle to the left = 3 m, since it is the shape of square, height of the triangle = 7 m.

Base of the triangle to the right = 16 - 7 ==> 9 m

height = 3 m

Area of shaded region = 1/2 x 3 x 7 + 1/2 x 9 x 3

= 21/2 + 27/2

= 10.5 + 13.5

= 24 square meter