AREA BETWEEN TWO CURVES USING INTEGRATION

Problem 1 :

Find the area bounded between the functions y = x³ - x & y = 3x.

Solution:

Let us find the point of intersection,

y = x³ - x ---> (1)

y = 3x ---> (2)

(1) = (2)

x³ - x = 3x

x³ - 4x = 0

x(x² - 4) = 0

x(x + 2)(x - 2) = 0

x = 0, x = 2 and x = -2

Using graphing calculator, find the area between the curves.

Problem 2 :

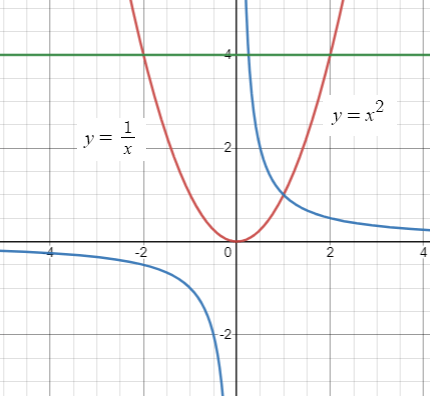
Find the area bounded between the functions y = x², y = 1/x & y = 4

Solution:

y = x² ----(1)  and y = 1/x ----(2)

x² = 1/x

(x³ - 1) / x = 0

x³ - 1 = 0

x³ = 1

x = 1

Problem 3 :

Find the area bounded by y = 2^x, y = 4^x and y = 1/x.

Solution:                                                                             

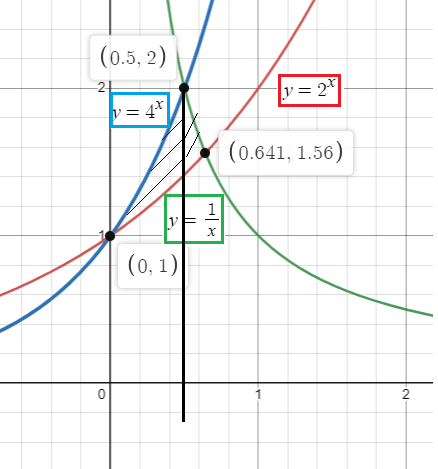
So, the required area is 0.63 square units.