AREA BETWEEN PARABOLA AND LINE USING INTEGRATION

Let f and g be defined over the interval [a, b] with g(x) ≤ f(x) for all x in [a, b] then the area A of the region bounded by there two curves and the lines x = a and x = b is given by

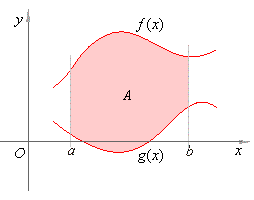
Sketch the graphs , shade the bounded region and find the area bounded by the given expressions.

Problem 1 :

y = x² + 1, y = x, x = -1 and x = 2

Solution:

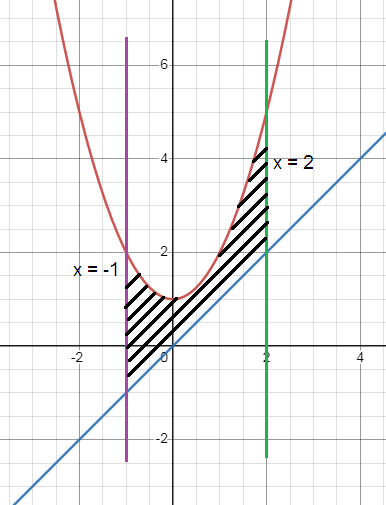
So, the required area is 4.5 square units.

Problem 2 :

y = √x and y = x/4

Solution:

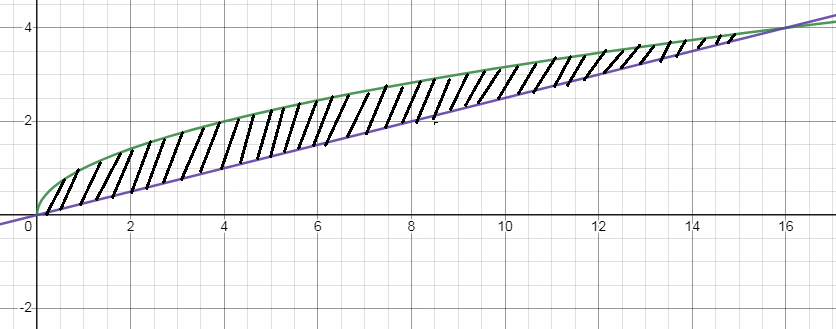
Let us find the point of intersection,

y = √x ---> (1)

y = x/4 ---> (2)

(1) = (2)

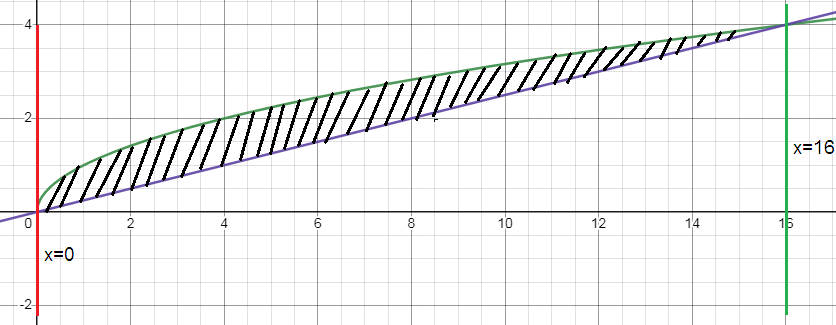
So, the required area is 32/3 square units.

Problem 3 :

x = 1/y², y = x and y = 2

Solution:

Let us find the point of intersection,

x = 1/y² ---> (1)

y = x ---> (2)

(1) = (2)

1/y² = y

y³ = 1

y = 1

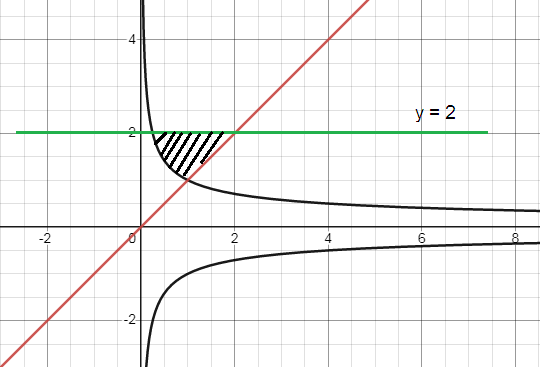
So, the required area is 1.5 square units.

Problem 4 :

x = 2 - y², y = -x

Solution:

Let us find the point of intersection,

x = 2 - y² ---> (1)

y = -x ---> (2)

(1) = (2)

-y = 2 - y²

y² - y - 2 = 0

(y - 2) (y + 1) = 0

y = -1 and y = 2

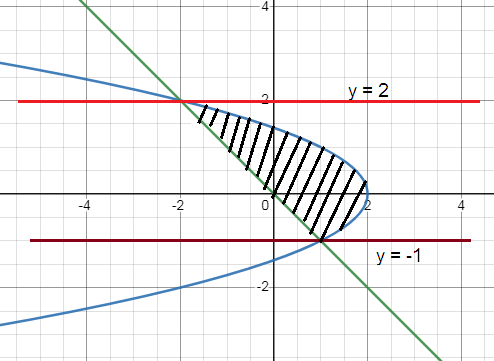
So, the required area is 4.5 square units.

Problem 5 :

y = x² and y = 4x

Use vertical rectangles (dx).

Solution:

Let us find the point of intersection,

y = x² ---> (1)

y = 4x ---> (2)

(1) = (2)

4x = x²

x² - 4x = 0

x(x - 4) = 0

x = 0 and x = 4

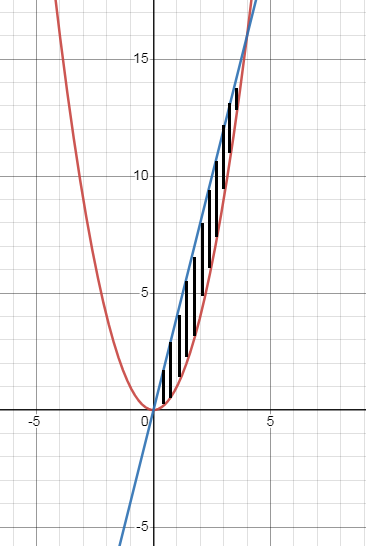
So, the required area is 32/3 square units.

Problem 6 :

y = x² and y = 4x

Use horizontal rectangles (dy).

Solution:

Let us find the point of intersection,

y = x²

x = √y ---> (1)

y = 4x 

x = 1/4 y ---> (2)

(1) = (2)

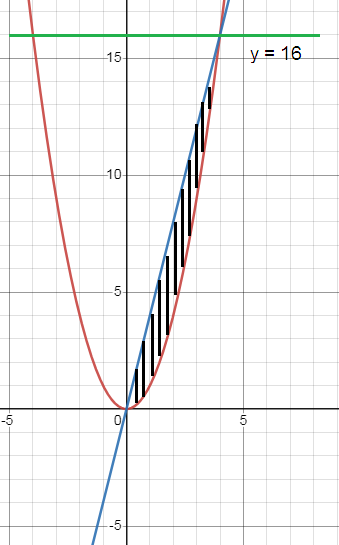
So, the required area is 32/3 square units.