AREA AND PERIMETER PROBLEMS INVOLVING POLYNOMIALS

Problem 1 :

What is the distance around the rectangle if the length is

3x² + 6x – 10

and the width is

3x + 5 ?

Solution :

The given shape is a rectangle, to find the distance around the shape rectangle is similar to find perimeter of the rectangle.

Length = 3x² + 6x – 10

Width = 3x + 5

Perimeter of rectangle = 2(length + width)

= 2[(3x² + 6x – 10) + (3x + 5)]

= 2[3x² + 6x + 3x - 10 + 5]

= 2[3x² + 9x - 5]

= 6x² + 18x - 10

So, the length around the shape is 6x² + 18x - 10.

Problem 2 :

If the perimeter of the pentagon below is 7x⁴ + 9x³ – 6x² + 10, what is the length of the missing side?

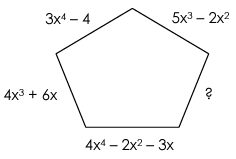
Solution :

Number of sides of the shape pentagon = 5

Perimeter =  7x⁴ + 9x³ – 6x² + 10

Adding the side lengths,

(3x⁴ - 4) + (5x³ - 2x²) + (4x³ + 6x) + (4x⁴ - 6x² - 3x) + unknown side = 7x⁴ + 9x³ – 6x² + 10 

(3x⁴+ 4x⁴+ 5x³ + 4x³- 2x² - 6x² + 6x - 3x - 4) + unknown side = 7x⁴ + 9x³ – 6x² + 10 

(7x⁴+ 9x³ - 8x² + 3x - 4) + unknown side = 7x⁴ + 9x³ – 6x² + 10 

unknown side

= 7x⁴ + 9x³ – 6x² + 10 - (7x⁴+ 9x³ - 8x² + 3x - 4)

= 7x⁴ - 7x⁴+ 9x³ - 9x³– 6x² - 8x² + 3x + 10 - 4

= -14x² + 3x + 6

Problem 3 :

If the perimeter of the square below is 12x⁵ – 8x² + 20x – 4, what is the length of one side?

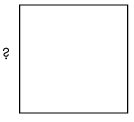
Solution :

Perimeter of square = 12x⁵ – 8x² + 20x – 4

Number of equal sides in the shape square = 4

Side length of square = Perimeter of square / 4

= (12x⁵ – 8x² + 20x – 4) / 4

Factoring 4 from the numerator, we get

= 4(3x⁵ – 2x² + 5x – 1) / 4

= 3x⁵ – 2x² + 5x – 1

Problem 4 :

Ana knows that the perimeter of her backyard is (6x² + 14x) feet. If the length of her backyard is (2x² + 3x – 7) feet, what is the width of her backyard?

Solution :

Let w be the width of backyard. But it is not clear that what shape it is exactly.

Perimeter = 6x² + 14x

Length = 2x² + 3x – 7

2[(2x² + 3x – 7) + w] = 6x² + 14x

Dividing by 2 on both sides

[(2x² + 3x – 7) + w] = (6x² + 14x)/2

[(2x² + 3x – 7) + w] = 3x² + 7x

w = (3x² + 7x) - (2x² + 3x – 7)

w = 3x² + 7x - 2x² - 3x + 7

By combining like terms , we get

w = 3x² - 2x²  + 7x - 3x + 7

w = x²+ 4x + 7

So, the required width of the rectangle is x²+ 4x + 7.

Problem 5 :

The area of the square below is represented by the expression 4x² + 4x + 1. The area of the rectangle is represented by the expression x² – 5x + 6. Using the diagram below, find the area of the shaded region.

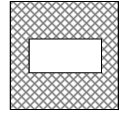
Solution :

Area of the square = 4x² + 4x + 1

Area of the rectangle = x² – 5x + 6

Area of unshaded region

= Area of the square - area of rectangle

= (4x² + 4x + 1) - (x² – 5x + 6)

= 4x² - x²+ 4x + 5x + 1 - 6

= 3x² + 9x - 5

Problem 6 :

A rectangular piece of wood has an area of

5x⁴ + 3x² – 6x + 8

If two identical circles are cut out of the wood and the area of EACH circle is

x² – 2

find the area of the remaining piece of wood. (Hint: Use the picture below.)

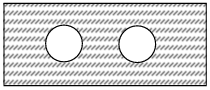
Solution :

Area of rectangular piece of wood = 5x⁴ + 3x² – 6x + 8

Area of one circle = x² – 2

Area of the remaining piece of wood

= Area of rectangle - 2(area of circle)

= 5x⁴ + 3x² – 6x + 8 - 2(x² – 2)

= 5x⁴ + 3x² – 6x + 8 - 2x² + 4

= 5x⁴ + 3x² - 2x²– 6x + 8 + 4

= 5x⁴ + x² – 6x + 12

So, area of the shaded part is 5x⁴ + x² – 6x + 12.

Problem 7 :

A circular plot of land has an area of

7x⁵ – x³ + 4x² + 9

If the walkway around this piece of land has an area of

x⁴ – 4x³ + 2x

what is the area of the land and walkway combined?

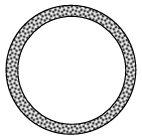
Solution :

Area of circular land = 7x⁵ – x³ + 4x² + 9

Area of walkway = x⁴ – 4x³ + 2x

Combined area = (7x⁵ – x³ + 4x² + 9) +(x⁴ – 4x³ + 2x)

= 7x⁵ + x⁴– x³ – 4x³ + 4x² + 2x + 9

= 7x⁵ + x⁴– 5x³ + 4x² + 2x + 9

Problem 8 :

The width of Adrian’s bedroom is (x – 5) feet. He knows that the length is four times the width. Find the perimeter of Adrian’s bedroom.

Solution :

Width of the bedroom = x - 5

Length = 4(width)

= 4(x - 5)

Perimeter of the bedroom = 2(length + width)

= 4(x - 5) + (x - 5)

= 4x - 20 + x - 5

= (5x - 25) feet

So, the required perimeter is (5x - 25) feet.