AREA AND PERIMETER OF SQUARE

What is the area of a square?

The area of a square is defined as the total number of unit squares in the shape of a square.

In other words, it is defined as the space occupied by the square.

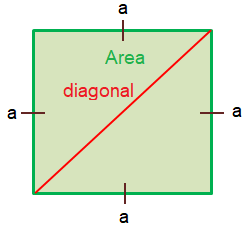
The formula for area of a square,

Area of a Square = a²

(where a is the side of a square)

Area of a square using diagonals = 1/2 × d²

What is the Perimeter of a Square?

The perimeter of a square is the distance covered by its four sides. 

Perimeter surrounds or outlines the shape in a two-dimensional plane.

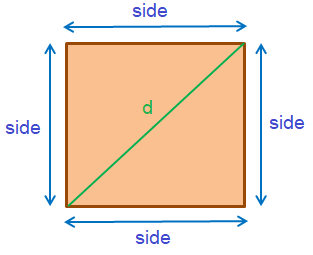
The formula for perimeter of a square,

Perimeter of a square = 4 side

Perimeter of a square using diagonals = 2√2 × d

Example 1 :

Find the perimeter of a square whose area is 120 m².

Solution :

Given, Area = 120 m².

Area of a Square = a²

120 = a²

a = √120

a = 10.95

Perimeter of a square = 4a

= 4(10.95)

Perimeter = 43.82 m

Example 2 :

Find the area of the square field whose perimeter is 240 m.

Solution :

Perimeter = 240 m.

Perimeter of a square = 4a

240 = 4a

240/4 = a

a = 60

Area of a Square = a²

Area = 60²

Area of the square field = 3600 m².

Example 3 :

A rope of length of 104 m is used to fence a square garden. What is the length of the side of the garden ?

Solution :

The length of rope is 104 m.

The perimeter of square fence is given as 104 m.

Perimeter of a square = 4a

104 = 4a

104/4 = a

a = 26 m

So the length of the side of the garden is 26 m.

Example 4 :

Lila has 16 square stamps of side 4 cm each. She glues them onto an envelope to form a bigger square. What area of the envelope does the bigger square cover?

Solution :

16 square shaped stamps can be arranged as 4 in each row.

So it forms 4 rows and 4 columns.

Side of the formed square s = 4 + 4 + 4 + 4

s = 16 cm

Area of a square =  s²

Area = 16²

= 256 cm²

So, the area of the bigger square is 256 cm².

Example 5 :

If the diagonal length of a square is 7 cm, find the square area, perimeter ?

Solution :

Area of a square using diagonals = 1/2 × d²

= 1/2 × 7²

= 1/2 × 49

Area = 24.5 cm²

Perimeter of a square using diagonals = 2√2 × d

=  2√2 × 7

Perimeter = 19.8 cm

Example 6 :

The diagonals of two squares are in the ratio 2 : 5. Find the ratio of their areas.

Solution :

Let the diagonal of 1^st square be 2x.

The diagonal of a square formula = a√2

a√2 = 2x

a = 2x/√2

a = 2x/√2 × √2/√2

= (2x√2)/(√2)²

= (2x√2)/2

a = √2x

Area of a square =  a²

= (√2x)²

Area = 2x²

Let the diagonal of 2^nd square be 5x.

The diagonal of a square formula = a√2

a√2 = 5x

a = 5x/√2

a = 5x/√2 × √2/√2

= (5x√2)/(√2)²

a = (5x√2)/2

Area of a square =  a²

= [(5x√2)/2]²

Area = (25x²)/2

Ratio of areas = 2x² : (25x²)/2

Multiplying 2 on both areas, we get

= 4 : 25

So, the ratio of their areas is 4 : 25.