APPLYING PROPERTIES TO FIND SIDE LENGTH OF RHOMBUS

In rhombus, 

• All sides are equal.
• Diagonals will bisect each other at right angles,
• The diagonals are equal.

Problem 1 :

Find the side length of rhombus given.

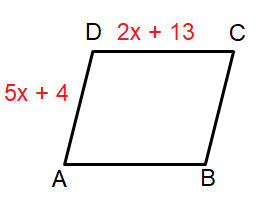
Solution :

Since the given shape is rhombus, all sides will have equal measure.

AD = DC

5x + 4 = 2x + 13

5x - 2x = 13 - 4

3x = 9

x = 9/3

x = 3

Applying the value of x, we get

AD = 5(3) + 4

AD = 15 + 4

AD = 19

Problem 2 :

Find the side length of the rhombus ABCD.

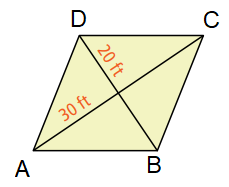
Solution :

Let E be the point of intersection of two diagonals. Considering the triangle DEC,

DE = 20 ft, EC = 30 ft

DC² = DE² + EC²

DC² = 20² + 30²

DC² = 400 + 900

DC² = 1300

DC = 10√13

Problem 3 :

The area of a rhombus is 150 cm². The length of one of its diagonal is 10 cm. The length of their other diagonal is .

(a)  25 cm   (b)  30 cm   (c) 35 cm    (d)  40 cm

Solution :

Area of rhombus = (1/2) x d₁ x d₂

(1/2) x 10 x d₂ = 150

d₂ = 150 / 5

d₂ = 30 cm

Problem 4 :

One of the diagonals of a rhombus is double the other diagonal. Its area is 25 sq.cm. The sum of the diagonal is 

(a)  10 cm   (b)  12 cm   (c) 15 cm    (d)  16 cm

Solution :

d₁ = 2d₂

(1/2) x d₁ x d₂ = 25

(1/2) x 2d₂ x d₂ = 25

d₂² = 25

d₂ = 5

then d1 = 2(5) ==> 10 cm

Sum of the diagonals = 10 + 5 ==> 15 cm

Problem 5 :

The perimeter of a rhombus is 56 m and height is 5 m. Its area is.

(a)  64 sq.cm   (b)  70 sq.cm   (c) 78 sq.cm    (d)  84 sq.cm

Solution :

Perimeter of rhombus (4a) = 56

a = 56/4

a = 14 cm

height = 5 cm

Area of rhombus = base x height

= 14 x 5

= 70 sq.cm

Problem 6 :

If the diagonals of a rhombus are 24 cm and 10 cm, find the area and perimeter of rhombus.

Solution :

Area of rhombus = (1/2) x d₁ x d₂

d₁ = 24 cm and d₂ = 10 cm

= (1/2) x 24 x 10

= 120 square cm

To find perimeter of rhombus, we should find the side length of rhombus.

side² = 12² + 5²

side² = 144 + 25

side² = 169

= √169

= 13

Perimeter of rhombus = 4(13)

= 52 cm

Problem 7 :

Each side of a rhombus is 26 cm and one of its diagonal is 48 cm long. The area of the rhombus is.

(a) 240 cm²       (b) 300 cm²  (c) 360 cm²    (d) 480 cm²

Solution :

The diagonals will bisect each other at right angle.

Half length of given diagonal = 24

half length of another diagonal = x

26² = 24² + x²

676 = 576 + x²

x² = 676 - 576

x² = 100

x = 10

Length of another diagonal = 20

Area of rhombus = (1/2) x 48 x 20

= 480 square cm

Problem 8 :

The length one diagonal of a rhombus is 80% of the other diagonal. The area of the rhombus is how many times the square of length of the other diagonal ?

(a) 4/5   (b)  2/5   (c)  3/4     (d)  1/4

Solution :

Let d₁ and d₂ be length of diagonals.

d₁ = 80% of d₂  ==> 0.80d₂

Area of rhombus = (1/2) x 0.80d₂ x d₂

= (1/2) x 0.80(d₂)²

= 0.40(d₂)²

= (40/100)(d₂)²

= 2/5(d₂)²

So, the answer is 2/5.