APPLICATION PROBLEMS ON VECTOR ALGEBRA WORD PROBLEMS

Problem 1 :

Prove by vector method that if a line is drawn from the center of the circle to the midpoints of a chord, then the line is perpendicular to the chord.

Solution :

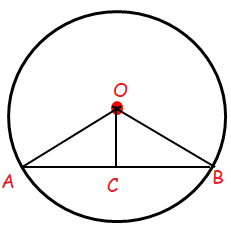
Let C be the midpoint of the chord AB. O is the center of circle.

OA = OB = radius.

So, OC is perpendicular to AB.

Problem 2 :

Prove by vector method that the median to the base of an isosceles triangle is perpendicular to the base.

Solution :

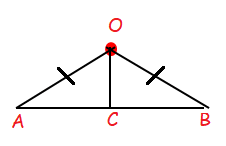
Since OC is the median AC = AB. The above triangle is isosceles triangle of equal sides OA and OB.

Then base of an isosceles triangle is perpendicular to its median.

Problem 3 :

Prove by vector method that an angle in a semicircle is a right angle.

Solution :

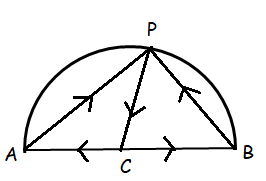
Angle in a semicircle is right angle.

Problem 4 :

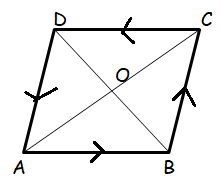
Prove by vector method that the diagonals of a rhombus bisect each other at right angles.

Solution :

In rhombus, all the sides will be equal.  

Problem 5 :

Using vector method, prove that if the diagonals of a parallelogram are equal, then it is a rectangle.

Solution :

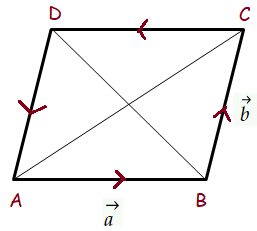
AB is perpendicular to AC, then it is rectangle.

Problem 6 :

Prove by vector method that the area of the quadrilateral ABCD having diagonals AC and BD is

Solution :

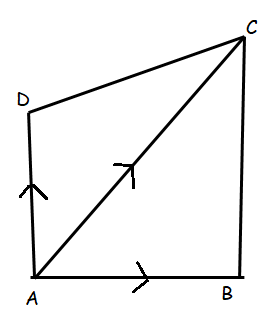
Area of quadrilateral ABCD

= Area of triangle ABC + area of ADC

Problem 7 :

Prove by vector method that the parallelogram on the same base between the same parallels are equal in area.

Solution :

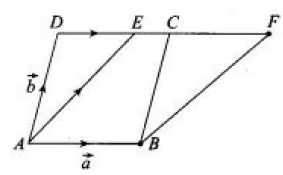
Problem 8 :

If G is the centroid of a triangle ABC, prove that 

Area of triangle GAB = area of triangle GBC = area of triangle GCA = 1/3 area of triangle ABC

Solution :

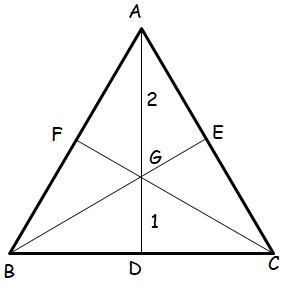
G is the centroid and it is dividing AG to GD in the ratio 2 : 1.