APPLICATION PROBLEMS ON PIECEWISE FUNCTION

Problem 1 :

A long distance telephone charges 99 cents for any call upto 20 minutes in length and 7 cents for each additional minute. Use bracket notation to write a formula for the cost C, of a call as function of its length time t in minutes. Graph the function. How much does it cost to talk for

i)  10 minutes ?

ii)  25 minutes ?

Solution :

Charges collected for long distance call = 0.99

For first 20 minutes (≤)

Let t be the additional minutes.

Charge for each additional minute = 0.07

Charge after t minute = 0.99 + 0.07t when t > 20

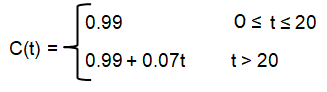
i)  10 minutes

t = 10 < 20

C(t) = 0.99

ii)  25 minutes

t = 25 > 20

C(t) = 0.99 + 0.07t

Applying t = 25 in the function above

C(25) = 0.99 + 0.07(25)

= 0.99 + 1.75

= 2.74

Problem 2 :

Suppose a carpet store sells carpet for $10 per square yard for the 100 square yards purchased, and then lower the price to $7 per square yard after the first 100 yards have been purchased. Find the function C = f(x), that gives the cost of purchasing any number of square yards of carpet between 0 and 200 square yards. How much does it cost for

i)  50 square yards ?

ii)  150 square yards ?

Solution :

Price of carpet per square yard = $10

for 100 square yards purchased

Let x be the area of the carpet purchased.

Cost spent for 100 yards = 100 (10) ==> 1000

After 100 yards, the cost spent = 0.07 (100 - x)

Cost spent for x area of the carpet = 1000 + 0.07 (100 - x)

for 100 ≤ x ≤ 200

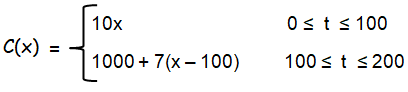
Problem 3 :

On a trip, the total distance (in miles) you travel in x hours is represented by a piecewise function 

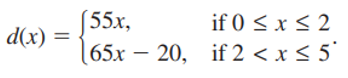
How far do you travel in 4 hours ?

Solution :

When x = 4, d(x) = 65x - 20

Applying the value of x, we get

d(4) = 65(4) - 20

= 260 - 20

= 240 miles

Problem 4 :

The total cost (in dollars) of ordering x custom shirts is represented by the piecewise function.

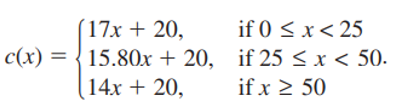
Determine the total cost of ordering 26 shirts.

Solution :

When x = 26

c(x) = 15.80x + 20

Applying the value of x, we get

c(26) = 15.80 (26) + 20

= 410.8 + 20

= 430.8

Problem 5 :

A car company charges $45 plus $0.20 per mile over 50 miles.

Give the equation for the cost of driving 0 ≤ m ≤ 50 miles

Give an equation to determine the cost of driving more than 50 miles (m > 50)

i)  How much will it cost you if you drive 20 miles ?

ii)  How much will it cost you if you drive 51 miles ?

Solution :

Let m be the number of miles driven.

Cost of driving 0 ≤ m ≤ 50 miles :

c(m) = 45

Cost of driving m > 50 miles :

c(m) = 45 + 0.20(m - 50)

i) When the distance to be covered = 20 miles.

This distance lies between 0 to 50, so the required cost is $45.

ii) When the distance to be covered = 51 miles.

c(m) = 45 + 0.20(m - 50)

= 45 + 0.20(51- 50)

= 45 + 0.20(1)

= $45.20

Problem 6 :

A cell phone company charges a monthly fee $9.95, and a usage  fee as follows.

• Less than 150 minutes : $0.40 per minute
• 150 to 300 minutes : $0.20 per minute
• Over 300 minutes : $0.10 per minute

i)  Write a piecewise function, C(m) for the cost of using m minutes.

ii) What is the total cost, if you use 200 minutes ?

iii) What is the total cost, if you use 350 minutes ?

Solution :

i) Let m be the number of minutes.

Monthly fee :

ii) What is the total cost, if you use 200 minutes ?

c(200) = 9.95 + 0.20(200 - 150)

= 9.95 + 0.20(50)

= $19.95

iii) What is the total cost, if you use 350 minutes ?

c(350) = 9.95 + 0.10(350 - 300)

= 9.95 + 0.10(50)

= $24.95