ANGLES INVOLVING TANGENTS OF CIRCLE

Angle between tangent and radius is 90 degree.

QM is tangent to ʘP at point M and QN is tangent to ʘP at point. Solve for the variable and determine the angle measures.

Problem 1:

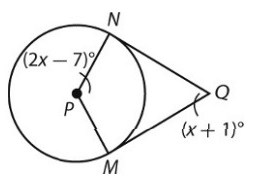
Solution :

PMNQ is quadrilateral. Sum of interior angles of quadrilateral is 360.

Since NQ and MQ are tangents, m∠QNP = m∠QMP = 90

x + 1 + 2x - 7 + 90 + 90 = 360˚

3x - 6 + 180 = 360˚

3x = 360 - 174

3x = 186

x = 186/3

x = 62˚

m∠NQM = x + 1

= 62 + 1

m∠NQM = 63˚

m∠NPM = 2x - 7

= 2(62) - 7

= 124 - 7

m∠NPM = 117˚

Problem 2 :

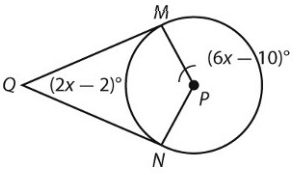
Solution :

2x - 2 + 6x - 10 + 90 + 90 = 360˚

8x - 12 + 180 = 360˚

8x = 360 - 168

8x = 192

x = 192/8

x = 24˚

m∠MQN = 2x - 2

= 48 - 2

m∠MQN = 46˚

m∠NPM = 6x - 10

= 6(24) - 10

= 144 - 10

m∠NPM = 134˚

Problem 3 :

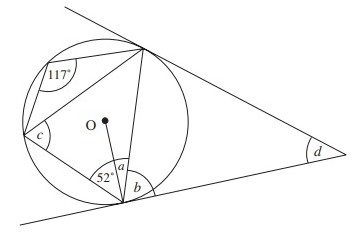
Solution :

117˚ + 52˚ + a = 180˚

169˚ + a = 180˚

a = 180˚ - 169˚

a = 11˚

a + b = 90˚

11 + b = 90˚

b = 90˚ - 11˚

b = 79˚

In the triangle,

b + b + d = 180

2b + d = 180

2(79) + d = 180

158 + d = 180

d = 180 - 158

d = 22

Using alternate segment theorem,

b = c = 79

Problem 4 :

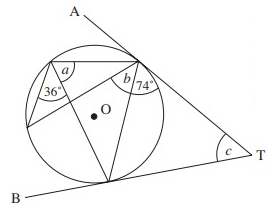
In the diagram, TA and TB are tangents. Find the angles a, b and c.

Solution :

Angles at the circumference of a circle subtended by the same arc are equal.

b = 36˚

74˚ + 74˚ + c = 180˚

148 + c = 180˚

c = 180˚ - 148˚

c = 32˚

Using alternate segment theorem,

a = 74

Problem 5 :

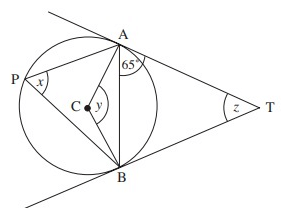
AT and BT are tangents to the circle, centre C.

P is a point on the circumference, as shown.

∠BAT = 65˚

Calculate the size of

a)x b)y c)z

Solution :

AT = BT

∠ABT = ∠BAT = 65˚

∠ABT + ∠BAT + ∠ATB = 180˚

65 + 65 + z = 180˚

z = 180˚ - 130˚

z = 50˚

∠CAB + ∠CBA + ∠ACB = 180˚

25˚ + 25˚ + y = 180˚

50 + y = 180˚

y = 180 - 50

y = 130˚

∠APB = 1/2∠ACB

= 1/2(130˚)

∠APB = 65˚

x = 65˚

ANGLES INVOLVING TANGENTS OF CIRCLE

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling