ANGLES AND ANGLE RELATIONSHIPS ON STRAIGHT LINES

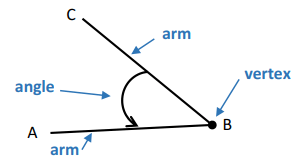
What is angle ?

A line is an infinite number of points between two end points. Where two lines meet or cross, they form an angle.

An angle is an amount of rotation. It is measured in degrees.

Different types of angles involving straight lines :

• Complementary angles Angles that add up to 90°
• Supplementary angles Angles that add up to 180°

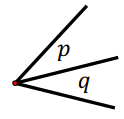
Adjacent angles :

Angle that have common vertex and a common arm.

Adjacent angles on a straight line add upto 180 degree.

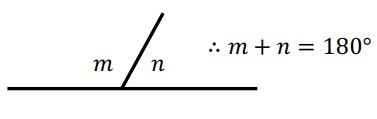
Perpendicular lines :

Lines that meet or cross at 90°

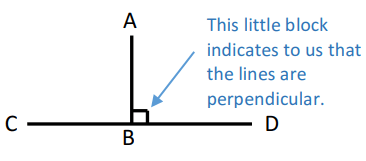
Here AB ⊥ CD.

Vertically opposite angles :

When two straight lines intersect the angles opposite each other are called vertically opposite angles.

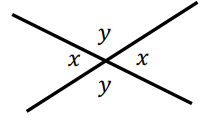
Vertically opposite angles are equal to each other.

Parallel lines and transversal

Transversals creates three important types of angles, namely:

1. Corresponding angles

2. Co-interior angles

3. Alternating angles

Corresponding angles are in the same position as each other.

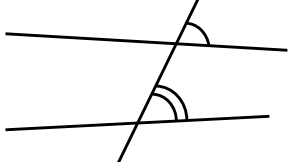
Co-interior angles are between the lines and on the same side of the transversal. They are “inside together”.

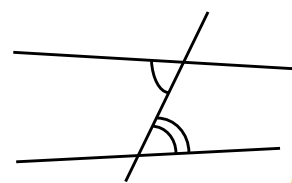
Alternate angles are between the lines and on alternate (opposite) sides of the transversal.

Problem 1 :

Find the value of each variable, providing reasons for your statements:

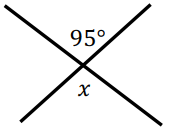
Solution :

Reason :

Vertically opposite angles are equal.

x = 95°

Problem 2 :

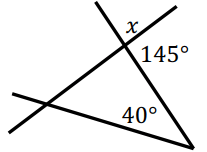
Solution :

Reason :

x and 145 are linear pairs.

x + 145 = 180

x = 180 - 145

x = 35°

Problem 3 :

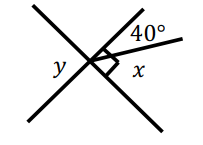
Solution :

Reason :

40 and x add upto 90 degree.

40 + x = 90

x = 90 - 40

x = 50°

Problem 4 :

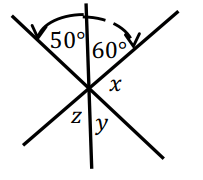
Solution :

Reason :

50°, 60° and x are supplementary angles.

50° + 60° + x = 180°

110° + x = 180°

x = 180° - 110°

x = 70°

x, y and z are supplementary angles.

x + y + z = 180

Applying the value of x, we get

70 + y + z = 180

y + z = 110

• 50 and y are vertically opposite angles.
• 60 and z are vertically opposite angles.

So, x = 70°, y = 50° and z = 60°

Problem 5 :

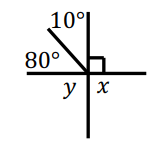
Solution :

Reason :

x and y are right angles.

x = 90° and y = 90°

Problem 6 :

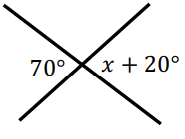
Solution :

Reason :

70° and x + 20° are vertically opposite angles.

70° = x + 20°

70° -  20° = x

x = 50°

Problem 7 :

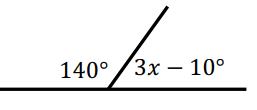
Solution :

Reason :

140° and 3x - 10 are supplementary angles.

140 + 3x - 10 = 180

130 + 3x = 180

3x = 180 - 130

3x = 50

x = 50/3°

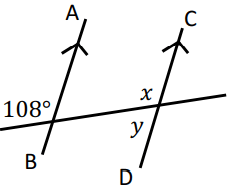
Problem 8 :

Solution :

Since the lines AB and CD are parallel, 108 and x are corresponding angles.

Reason :

x and y are supplementary.

x = 108

x + y = 180

108 + y = 180

y = 180 - 108

y = 72

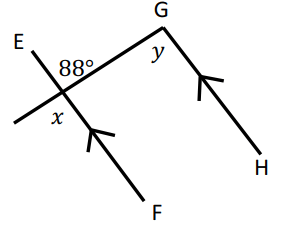
Problem 9 :

Solution :

Reason :

x and 88° are vertically opposite angles.

Since the lines EF and HG are parallel, x and y are corresponding angles.

x = 88 and y = 88.