ANGLE SUBTENDED BY AN ARC AT THE CENTER OF A CIRCLE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Theorem :
When two angles subtended by the same arc, the angle at the center of the circle is twice the angle at the circumference
Considering the circle with center O, now placing the points A, B and C on the circumference.
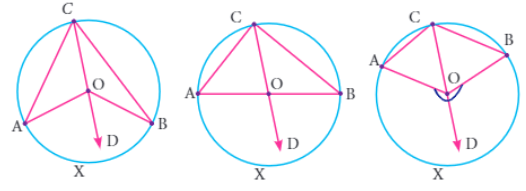
∠ACO = ∠OAC
∠BCO = ∠OBC
∠AOD = Exterior angle of the triangle
∠AOD = ∠ACO + ∠OAC ----(1)
∠BOD = ∠BCO + ∠OBC ----(2)
(1) + (2)
∠AOD + ∠BOD = (∠ACO + ∠OAC) + (∠BCO + ∠OBC)
∠AOB = (∠ACO + ∠OAC) + (∠BCO + ∠OBC)
∠AOB = 2∠OCA + 2∠OCB
∠AOB = 2(∠OCA + ∠OCB)
∠AOB = 2∠ACB
Work out the
size of each angle marked with a letter. Give reasons for your answers.
Problem 1 :
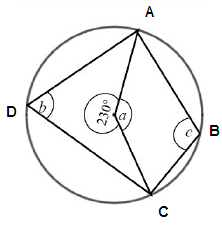
Solution :
∠AOC + 230˚ = 360˚
∠AOC = 360 - 230
∠AOC = 130˚
a = 130˚
∠ADC = 1/2 ∠AOC
∠ADC = 1/2(130)
∠ADC = 65˚
b = 65˚
Since ABCD is a cyclic quadrilateral, the opposite angles add upto 180.
∠ABC + ∠ADC = 180˚
∠ABC + 65 = 180˚
∠ABC = 180 - 65
∠ABC = 115˚
c = 115˚
Problem 2 :
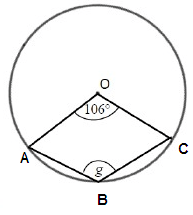
Solution :
∠AOC = 360 - 106 = 254˚
2∠ABC = reflex of ∠AOC
Reflex of ∠AOC = 2g
g = reflex of ∠AOC /2
= 254/2
= 127˚
So, the value of g is 127˚.
Problem 3 :
P, Q and R are points on the circumference of a circle, center, O. Angle PRQ = 64˚. SP and SQ are tangents to the circle at the points P and Q respectively.
Work out the size of angle
i) PSQ ii) PQO iii) POS iv) QSO
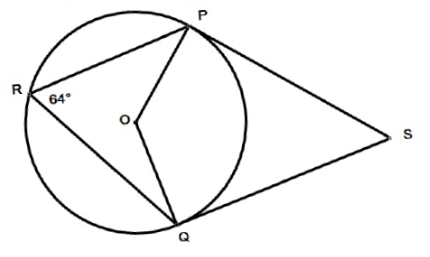
Solution :
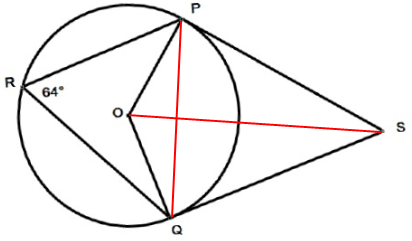
∠POQ = 2 ∠PRQ
∠POQ = 2(64˚)
∠POQ = 128˚
i) PSQ :
∠PSQ + ∠POQ = 180˚
∠PSQ + 128 = 180
∠PSQ = 180 - 126
∠PSQ = 52˚
∠OSP = 52˚/2 ==> 26
In triangle PSQ,
∠SPQ + ∠SQP + ∠PSQ = 180
Here ∠SPQ = ∠SQP (SP and SQ are tangents drawn from the external point, they will have same length).
2∠SPQ + 52 = 180
∠SPQ = 64
ii) PQO :
∠PQO = ∠SQO - ∠SQP
∠PQO = 90 - 64
∠PQO = 26
iii) POS :
∠OPS + ∠OSP + ∠POS = 180
90 + 26 + ∠POS = 180
∠POS = 180 - 116
∠POS = 64
iv) QSO :
∠QSO = 1/2 ∠PSQ
= 1/2(52)
∠QSO = 26˚
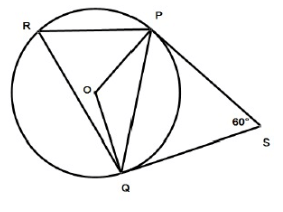
Problem 4 :
P, Q and R are points on the circumference of a circle, center, O. Angle PSQ = 60˚. SP and SQ are tangents to the circle at the points P and Q respectively.
a. Work out the size of angle
i) QPS ii) PQO iii) PRQ iv) POQ
b. what type of triangle is PQS?
c. Given that angle OQR = 10, work out the size of angle OPR.
Solution :
a. Given, SP = SQ
i) QPS :
∠PSQ = 60˚, so ∠QPS = ∠PQS
∠QPS = ∠PQS = 1/2(180 - 60)
∠QPS = 60˚
ii) PQO :
∠PQO = ∠SQO - ∠SQP
= 90˚ - 60˚
∠PQO = 30˚
iii) POQ :
∠POQ = 360˚ - (∠PSQ + ∠SPO + ∠SQO)
= 360˚ - (60 + 90 + 90)
= 360 - 240
∠POQ = 120˚
iv) PRQ :
∠PRQ = 1/2 ∠POQ
= 1/2(120)
∠PRQ = 60˚
b. Given, PSQ = 60˚
SP = SQ
So, PSQ is an equilateral triangle.
c. ∠OQR = 10˚
∠RQP = ∠OQR + ∠OQP
= 10˚ + 30˚ = 40˚
∠RPQ = 180˚ - ∠RQP - ∠QRP
= 180 - 40 - 60 = 80˚
∠QPO = ∠SPO - ∠SPQ
= 180 - 60 = 30˚
∠OPR = ∠RPQ - ∠SPO
∠OPR = 80 - 30
∠OPR = 50˚
Problem 5 :
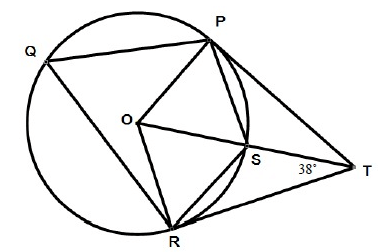
P, Q, R and S are points on the circumference of a circle, center, O. PT and TR are tangents to the circle. OST is a straight line.
Angle OTR = 38˚
Find the size of the angle:
i) ROT ii) PQR iii) SRT iv) PSO v) PST
Solution :
i) ROT :
∠TPO = ∠TRO = 90˚
90 + 38 + ∠ROT = 180˚
128 + ∠ROT = 180
∠ROT = 180 - 128
∠ROT = 52˚
ii) PQR :
∠POR = 2 ∠ROT
= 2(52˚)
∠POR = 104˚
∠PQR = 1/2 ∠POR
= 1/2 (104˚)
∠PQR = 52˚
iii) SRT :
OR = OS
∠ORS = ∠OSR
∠RSO = 1/2(∠ORS + ∠RSO)
= 1/2(180 - 52)
∠RSO = 64˚
∠SRT = ∠RSO - ∠OTR
∠SRT = 64˚ - 38˚
∠SRT = 26˚
iv) PSO :
∠PSO = ∠RSO = 64˚
v) PST :
∠PST = ∠RST
= 180˚ - ∠RSO
= 180˚ - 64˚
∠PST = 116˚
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling