ANGLE OF ELEVATION AND DEPRESSION QUESTIONS

Problem 1 :

Find the height of a vertical cliff if the angle of elevation is 25° to the top from a point which is 235 m from the base of the cliff.

Solution:

Let x be the height of a vertical cliff.

So, height of the vertical cliff is 109.58 m.

Problem 2 :

What angle will a 5 m ladder make with a wall if it reaches 4.2 m up the wall?

Solution:

Problem 3 :

The angle of elevation to the top of a lighthouse 25 m above sea-level from a fishing boat is 6°. Calculate the horizontal distance of the boat from the lighthouse.

Solution:

So, horizontal distance of the boat from the lighthouse is 238.09 m.

Problem 4 :

The angle of elevation from point A on horizontal ground to the top of a 20 m high pole is 35°. A rope is attached from A to the top of the pole. Find the length of the rope.

Solution:

So, length of the rope is 34.90 m.

Problem 5 :

A rectangular gate has a diagonal strut of length 3 m and an angle between the diagonal and a side is 28°. Find the length of the longer side of the gate.

Solution:

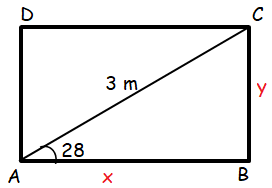
Let x be the longer side and y be the shorter side.

In triangle ABC,

cos θ = Adjacent side / Hypotenuse

cos θ = AB/AC

cos 28 = x/3

x = 3 cos 28

x = 3(0.882)

x = 2.646

So, the length of longer side is 2.646 m.

Problem 6 :

From a vertical cliff 80 m above sea level, a fishing boat is observed at an angle of depression of 6°. How far out to sea is the boat?

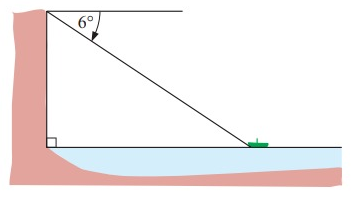
Solution:

So, the distance of the boat to the cliff is 762 m.

Problem 7 :

A railway line goes up an incline of constant angle 4° over a horizontal distance of 4 km. How high is it above the horizontal at the end of the incline?

Solution:

= 0.279 × 1000

= 279 m

Problem 8 :

At the entrance to a building there is a ramp for wheelchair access. The length of the ramp is 5 metres, and it rises to a height of 0.6 metres. Find the angle θ that the ramp makes with the ground.

Solution :

Problem 9 :

The roof of a bus shelter is supported by a metal strut 2.5 m in length, attached to the back wall of the shelter at an angle of 40˚. Calculate how far below the roof of the shelter the strut is attached to the wall.

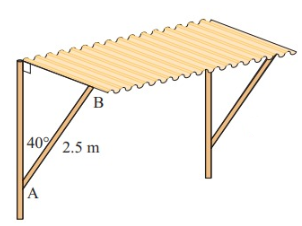
Solution :

Hypotenuse = 2.5 m

cos 𝜃 = adjacent side / hypotenuse 

cos 40 = Adjacent side / 2.5

Adjacent side = 2.5 cos 40

= 2.5 (0.766)

= 1.92 m

Problem 10 :

The diagram alongside shows a goalpost which has snapped in two after being hit by lightning. The top of the post is now resting 15 m from its base at an angle of 25˚. Find the height of the goal post before it snapped.

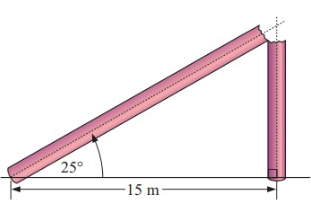
Solution :

Height = Opposite side

tan 𝜃 = Opposite side/adjacent side

tan 25 = Opposite side / 15

Opposite side = 15 (tan 25)

= 6.99

Height of the goal post before it snapped = 15 + 6.99

= 21.99

Approximately 23 m.