ANGLE BISECTOR THEOREM WORKSHEET

Problem 1 :

In the ΔABC shown below, find the length of AD.

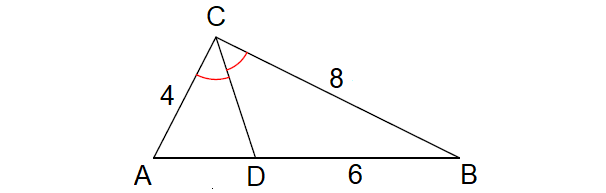
Solution :

Since CD is the angle bisector of ∠C, by Angle Bisector Theorem,

AD/DB = CA/CB

Let AD = x, DB = 6, AC = 4 and BC = 8

x/6 = 4/8

x/6 = 1/2

Doing cross multiplication, we get

2x = 6(1)

2x = 6

x = 6/2

x = 3

AD = 3 cm

So, the measure of AD is 3 cm.

Problem 2 :

In the ΔABC shown below, find the length of CD.

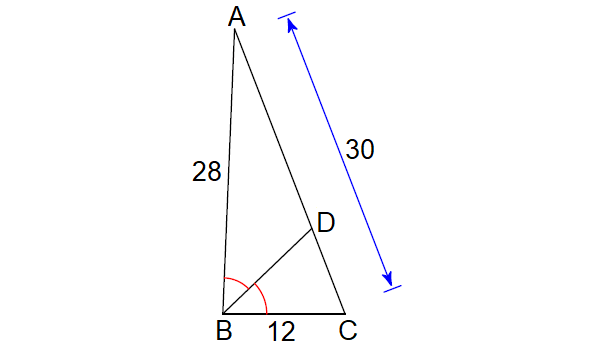
Solution :

Find the length of  DA :

DA = CA - CD

= 30 - x

Since BD is the angle bisector of ∠B, by Angle Bisector Theorem,

CD/DA = BC/BA

Let CD = x, DA = 30 - x, BC = 12 and AB = 28

x/(30 - x) = 12/28

x/(30 - x) = 3/7

Doing cross multiplication, we get

7x = 3(30 - x)

7x = 90 - 3x

Add 3x to both sides.

10x = 90

Divide both sides by 10.

x = 9

CD = 9

So, the measure of CD is 9 cm.

Problem 3 :

Solve for x.

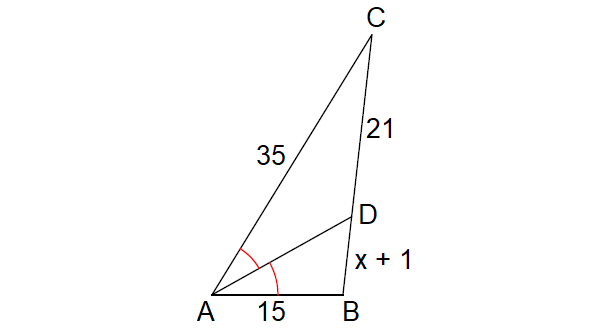
Solution :

Since AD is the angle bisector of ∠A, by Angle Bisector Theorem,

BD/DC = AB/AC

BD = x + 1, DC = 21, AB = 15 and AC = 35

(x + 1)/21 = 15/35

(x + 1)/21 = 3/7

7(x + 1) = 3(21)

7x + 7 = 63

Subtract 7 from both sides.

7x = 56

Divide both sides by 7.

x = 56/7

x = 8

Problem 4 :

Solve for x.

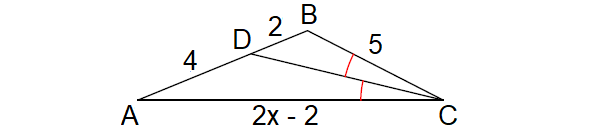
Solution :

Since CD is the angle bisector of ∠C, by Angle Bisector Theorem,

BD/DA = CB/CA

BD = 2, DA = 4, BC = 5 and AC = 2x - 2

2/4 = 5/(2x - 2)

Doing cross multiplication, we get

2(2x - 2) = 5(4)

4x - 4 = 20

4x = 20 + 4

4x = 24

x = 24/4

x = 6

Problem 5 :

Solve for x.

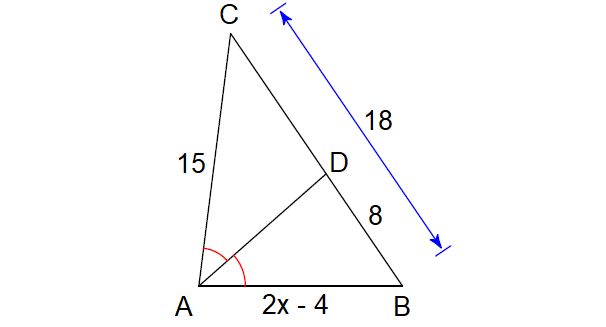
Solution :

Find the length of DC :

DC = BC - DC

= 18 - 8

= 10

Since AD is the angle bisector of ∠A, by Angle Bisector Theorem,

BD/DC = AB/AC

Substitute.

8/10 = (2x - 4)/15

4/5 = (2x - 4)/15

15(4) = 5(2x - 4)

60 = 10x - 20

Add 20 to both sides.

80 = 10x

Divide both sides by 10.

8 = x

Problem 6 :

Solve for x.

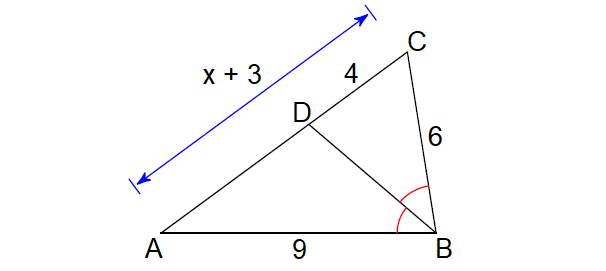
Solution :

Find the length of DA :

DA = CA - CD

= (x + 3) - 4

= x + 3 - 4

= x - 1

Since BD is the angle bisector of ∠B, by Angle Bisector Theorem,

CD/DA = BC/BA

Substitute.

4/(x - 1) = 6/9

4/(x - 1) = 2/3

3(4) = 2(x - 1)

12 = 2x - 2

Add 2 to both sides.

14 = 2x

Divide both sides by 2.

7 = x

Problem 7 :

In triangle ABC, AE is the external bisector of ∠A , meeting BC produced at E. If AB = 10 cm, AC = 6 cm and BC = 12 cm, then find CE.

Solution :

In triangle ABC, AE is the external bisector of ∠A meeting BC produced at E. Let CE = x cm. Now, by the angle bisector theorem, we have

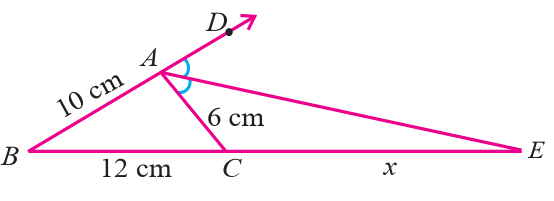
BE/CE = AB/AC

BE = BC + CE

BE = 12 + x

(12 + x)/x = 10/6

6(12 + x) = 10x

72 + 6x = 10x

72 = 10x - 6x

72 = 4x

x = 72/4

x = 18

So, the length of CE is 18 cm.

Problem 8 :

8)  In triangle PQR, RS is the bisector of ∠R. If PQ = 6 cm, QR = 8 cm, RP = 4 cm then PS is equal to

(A) 2 cm    (B) 4 cm     (C) 3 cm     (D) 6 cm

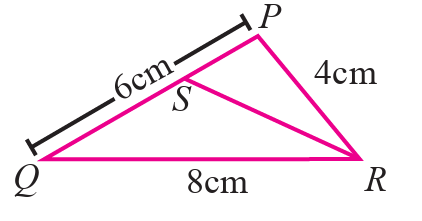
Solution :

Let QS = x, then PS = 6 - x

QR = 8 cm and PR = 4 cm

PS/QS = RP/RQ

(6 - x) / x = 4 / 8

8(6 - x) = 4x

48 - 8x = 4x

48 = 4x + 8x

48 = 12x

x = 48/12

x = 4

PS = 6 - 4 ==> 2 cm

So, the length of PS is 2 cm, option (A) is correct.

Problem 9 :

 In figure, if AB/AC = BD/DC,  ∠B = 40 degree and ∠C = 60 degree, then ∠BAD =  

(A) 30°    (B) 50°     (C) 80°     (D) 40°

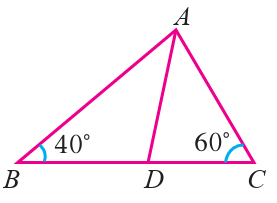
Solution :

In triangle, the sum of interior angles of triangle is equal to 180 degree

∠BAC + ∠ABC + ∠ACB = 180

∠BAC = ∠BAD + ∠DAC

and ∠BAD and ∠DAC are equall.

∠BAD + ∠DAC + 40 + 60 = 180

∠BAD + ∠DAC + 100 = 180

∠BAD + ∠DAC = 180 - 100

∠BAD + ∠DAC = 80

2∠BAD = 80

∠BAD = 80/2

∠BAD = 40

So, otpion D is correct.