AMPLITUDE PERIOD MAXIMUM AND MINIMUM OF SINE FUNCTIONS

Amplitude Period Maximum and Minimum of Sine Functions

A periodic function is one which repeats itself over and over in horizontal direction.

What is period ?

The period of a periodic function is the length of one repetition or cycle

What is amplitude ?

The amplitude is the vertical distance between a maximum point and the principal axis.

What is maximum and minimum ?

• The maximum points occurs at the top of the crest.
• The minimum points occurs at the bottom of a through.

What is principal axis or man line ?

The graph oscillates about horizontal line called the principal axis or mean line.

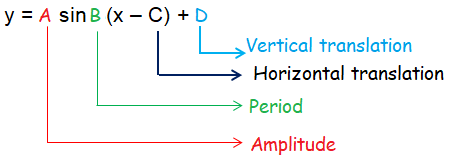
• The amplitude is |A|
• Period is 2π/B, for B > 0

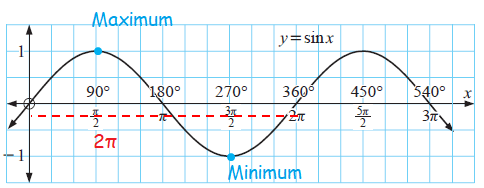
For the following sine functions find 

i) amplitude 

ii) period

iii)  maximum and minimum of y-values and corresponding x-values

iv) Graph two full periods of each function.

Problem 1 :

f(x) = 4 sin x

Solution :

f(x) = 4 sin x

f(x) = A sin B(x - C) + D

Comparing the given function with function above, we get

Amplitude (A) = 4, B = 1, period = 2π/1 ==> 2π

Midline y = 0

Length of 2 periods = 2 (2π) = 4π

(0, 0) (π/2, 4) (π, 0) (3π/2, -4) (2π, 0)

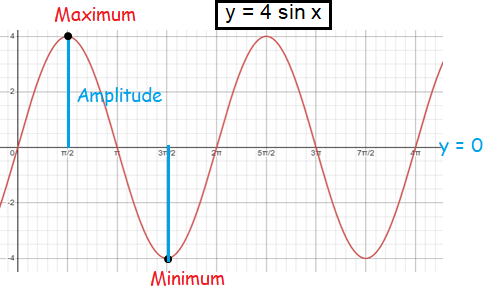
Maximum = 4 at x = π/2

Minimum = -4 at x = 3π/2

Problem 2 :

f(x) = 3 sin x + 2

Solution :

f(x) = 3 sin x + 2

f(x) = A sin B(x - C) + D

Comparing the given function with function above, we get

Amplitude (A) = 3, B = 1, period = 2π/1 ==> 2π

Midline y = 2, vertical translation of 2 units up.

Length of 2 periods = 2 (2π) = 4π

x = 2π

f(x) = 3 sin 2π + 2

f( 2π) = 3(0) + 2

= 2

The points are :

(0, 2)  (π/2, 5) (π, 2) (3π/2, -1) and (2π, 2)

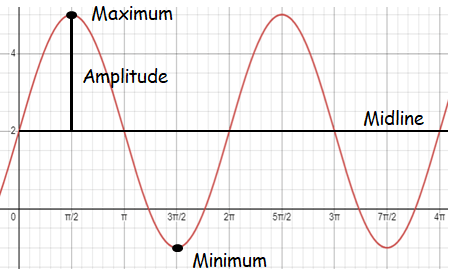
Maximum = 5 at x = π/2

Minimum = -1 at x = 3π/2

Problem 3 :

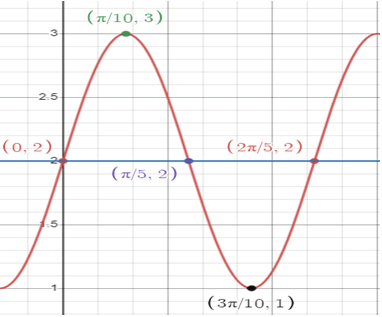
f(x) = sin (5x) + 2

Solution :

f(x) = sin (5x) + 2

f(x) = A sin B(x - C) + D

Comparing the given function with function above, we get

Amplitude (A) = 1, B = 5, period = 2π/5

Dividing 2π/5 by 4, we get 2π/20 ==> π/10

So, x values will be x = 0, π/10, 2π/10, 3π/10, 4π/10, .......

Midline y = 2, vertical translation of 2 units up.

f(x) = sin (5x) + 2

x = 4π/10

f(4π/10) = sin (20π/10) + 2

f(4π/10) = sin (2π) + 2

= 0 + 2

= 2

The points are :

(0, 2)  (π/10, 3) (2π/10, 2) (3π/10, 1) and (4π/10, 2)

Maximum = 3 at x = π/10

Minimum = 1 at x = 3π/10