ADJACENT ANGLES AND LINEAR PAIR

Two angles which have same vertex and share a common arm are called adjacent angles.

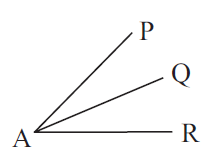
∠PAQ and  ∠QAR are adjacent angles.

Adjacent at a point :

The sum of the sizes of the angles at a point is 360 degree

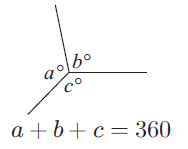
Adjacent angles on a straight line :

The sum of sizes of the angles on a line is 180 degree. The angles are supplementary.

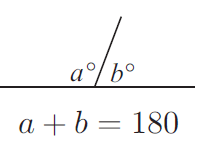
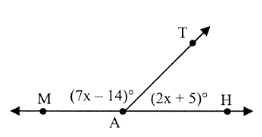
Problem 1 :

x = _____

m ∡MAT = _____

Solution:

7x - 14 + 2x + 5 = 180°

9x - 9 = 180°

9x = 189

x = 21°

m ∡MAT = 7x - 14

7(21) - 14

= 147 - 14

m ∡MAT = 133

Problem 2 :

x = _____

m ∡PIR = _____

m ∡RIM = _____

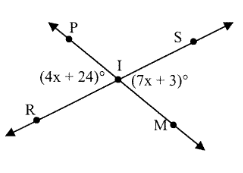
Solution:

4x + 24 = 7x + 3 (vertically opposite)

7x - 4x = 24 - 3

3x = 21

x = 7

m∡PIR = 4x + 24

= 4(7) + 24

m ∡PIR = 52°

Now,

∡PIR + ∡RIM = 180° (linear pair)

52° + ∡RIM = 180°

∡RIM = 180 - 52

∡RIM = 128°

Problem 3 :

p = _____

m ∡BNK = _____

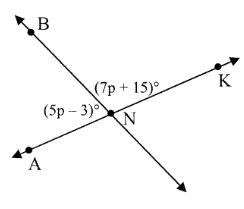
Solution:

∡ANB + ∡BNK = 180°

5p - 3 + 7p + 15 = 180°

12p + 12 = 180°

12p = 168°

p = 168/12

p = 14

∡BNK = 7p + 15

= 7(14) + 15

= 98 + 15

∡BNK = 113°

Problem 4 :

Which equation is set up correctly?

A) 2x + 5 + 3x - 8 - 180        B) 2x + 5 + 3x - 8 = 5x - 3

C) 2x + 5 + 3x - 8 = 90         D) 2x + 5 = 3x - 8

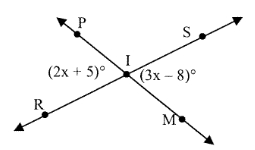
Solution:

If the two sides of an angle are opposite extensions of the other and they have common vertices, then they are vertical angles.

Vertical angles are equal.

So,

2x + 5 = 3x - 8

So, option (D) is correct.

Problem 5 :

Which equation is set up correctly?

A) 3x + 8 + 5x - 2 = 180       B) 3x + 8 + 5x - 2 = 8x + 6

C) 3x + 8 + 5x - 2 = 90         D) 10 = 2x

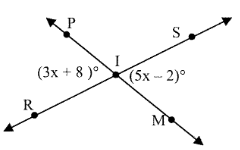
Solution:

If the two sides of an angle are opposite extensions of the other and they have common vertices, then they are vertical angles.

Vertical angles are equal.

So,

3x + 8 = 5x - 2

8 + 2 = 5x - 3x

10 = 2x

So, option (D) is correct.