ADDING AND SUBTRACTING FRACTION AND INTEGERS

To combine the integer and fraction, we can use the following ways.

(i) Considering the integer as fraction by considering its denominator is 1.

(ii)  Taking the denominator of the fraction and multiply it by the integer and simplify.

Method 1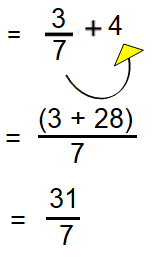

Method 2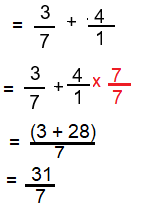

Problem 2 :

 4 - 2  1/4

Solution :

=  4 - 2  1/4

= (16 – 9)/4

= 7/4

= 1  3/4

Problem 3 :

 1 - 3/8

Solution :

= (8 – 3)/8

= 5/8

Problem 4 :

5/6 + 3/5 + 1/3

Solution :

= 5/6 + 3/5 + 1/3

Least common multiple of 6, 5 and 3 is 30.

= (5/6 × 5/5) + (3/5 × 6/6) + (1/3 × 10/10)

= 25/30 + 18/30 + 3/30

= (25+18+3)/30

= 53/30

= 1  23/30

Problem 5 :

2/5 + 3/8 + 1

Solution :

= 2/5 + 3/8 + 1

Least common multiple of 5, 8 and 1 is 40.

= (2/5 × 8/8) + (3/8 × 5/5) + (1/1 × 40/40)

= 16/40 + 15/40 + 40/40

= (16 + 15 + 40)/40

= 71/40

= 1 31/40

Problem 6 :

3/4 + 1/6 - 1/2

Solution :

= 3/4 + 1/6 - 1/2

Least common multiple of 4, 6 and 2 is 12.

= (3/4 × 3/3) + (1/6 × 2/2) - (1/2 × 6/6)

= 9/12 + 2/12 - 6/12

= (9 + 2 - 6)/12

= 5/12

Problem 7 :

1/3 - 2/5 + 1/4

Solution :

= 1/3 - 2/5 + 1/4

Least common multiple of 3, 5 and 4 is 60.

= (1/3 × 20/20) - (2/5 × 12/12) + (1/4 × 15/15)

= 20/60 - 24/60 + 15/60

= (20 - 24 + 15)/60

= 11/60

Problem 8 :

What fraction of 4/7 must be added to itself to make the sum 1  1/14 ?

a)  1/2    b)  4/7     c)  7/8     d)  15/14

Solution :

Required fraction to be added = 1  1/14 - 4/7

= 1 + 1/14 - 4/7

= 1 + 1/14 - 8/14

= 1 - 7/14

= 1 - 1/2

= 1/2

So, the required fraction is 1/2.

Problem 9 :

In an examination, a student was asked to find 3/14 of a certain number. By mistake he found 3/4 of that number . His answer was 150 more than the correct answer. The number is 

a)  180    b)  240     c)  280     d)  290

Solution :

Exactly we have to find 3/14 of the required number. By mistake he found 3/4 of that number.

3/4 of that number = 3/14 of that number + 150

3/4 of that number - 3/14 of that number = 150

(3/4 - 3/14) of that number = 150

LCM of 4, 14 is 28.

(21 - 6)/28 of that number = 150

15/28 of that number = 150

the required number = 150 / (15/28)

= 150 x (28/15)

= 10 x 28

= 280

So, option c is correct.

Problem 10 :

A students was asked to find the value of 3/8 of a sum of money. The student made a mistake by dividing the sum by 3/8 and thus got an answer which exceeded the correct answer by 55. The correct answer was.

a)  9    b)  18     c)  24     d)  64

Solution :

Sum of the money be a

a / (3/8) = 3/8 of a + 55

8a/3 = 3a/8 + 55

8a/3 - 3a/8 = 55

(64a - 9a)/24 = 55

55a/24 = 55

a = 55(24/55)

a=  24

So, the required sum of money is 24. Option c is correct.

Problem 11 :

An institue organized a fete and 1/5 of the girls and 1/8 of boys participated in the same. What fraction fo the total number of students took part in the fete ?

a)  2/13    b)  13/40     c)  Data inadequate     d)  none

Solution :

Total number of students = Number of girls + Number of boys

= 1/5 + 1/8

LCM (5, 8) = 40

= (1/5) x (8/8) + (1/8) x (5/5)

= 8/40 + 5/40

= (8 + 5)/40

= 13/40

So, option b is correct.

Problem 12 :

A tank is 2/5 full. If 16 liters of water is added to the tank, it becomes 6/7 full. The capacity of the tank is 

a)  28 liters    b)  32 liters     c)  35 liters      d)  42 liters

Solution :

Let a be the capacity of the tank.

2/5 of a is the quantity of tank now.

2/5 of a + 16 = 6/7 of a

2/5 of a - 6/7 of a = -16

(2/5 - 6/7) of a = -16

LCM of 5, 7 is 35

(14 - 30)/35  of a = -16

- 16/35 of a = -16

-16a / 35 = -16

a = 16(35/16)

a = 35

So, the capacity of the tank is 35 liters.

Problem 13 :

The highest score in an inning was 3/11 of a total and next highest was 3/11 of the remainder. IF the scores differed by 9, the total score was.

a)  110        b)  121       c)  132     d)  143

Solution :

Let a be the total score.

The first highest score = 3/11 of total score

= 3/11 of a

= 3a/11

The next highest score = 3/11 of remaining of total score

= 3/11 of 8/11 of a

= 3/11(8/11) a

= 24a/121

3a/11 - 24a/121 = 9

(33a - 24a)/121 = 9

9a/121 = 9

a = 9(121/9)

a = 121

So, option b is correct.