SMO JUNIOR SECTION 2015

Problem 1 :

Among the five numbers 5/9, 4/7, 3/5, 6/11 and 13/21 which one has the smallest value ?

(A)  5/9     (B) 4/7     (C)  3/5   (D)  6/11     (E)  13/21

Solution

Problem 2 :

Adrian, Biliy, Christopher, David and Eric are the five starters of a school's basketball team. Two among the five shoot with their left hand while the rest shoot with their right hand. Among the five, only two are more than 1.8 meters in height. Adrian and Billy shoot with the same hand, but Christopher and David shoot with different hands. Biliy and Christopher are respectively the shortest and tallest member of the team, while Adrian and David have the same height. Who is more than 1.8 meters tall and shoots with his left hand? 

(a)  None (B) Only Christopher (C) Only Eric

Christopher and Eric (E) Not enough information to ascertain

Solution

Problem 3 :

How many ways are there to arrange 3 identical blue balls and 2 identical red balls in a row if the two red balls must always be next to each other?

(A) 2   (B) 4    (c) 5    (D) 10    (E) 20

Solution

Problem 4 :

If. a,b and c are positive real numbers such that

Solution

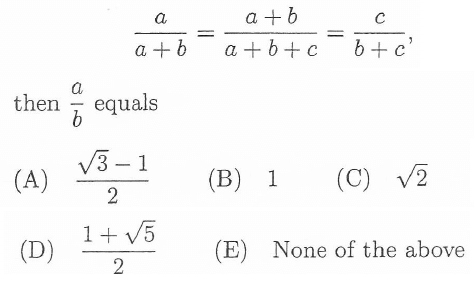
Problem 5 :

In the figure below, each distinct letter represents a unique digit such that the arithmetic sum holds. What is the digit represented by the letter B?

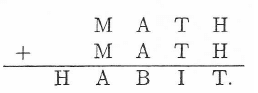
(A) 0   (B) 2    (c) 4    (D) 6    (E) 8

Solution

Problem 6 :

Find the minimum value of the function

2015  -  [10/(x² -4x + 5)]

(A) 2000   (B) 2005    (c) 2010   

(D) 2013    (E) None of these

Solution

Problem 7 :

It is known that 99900009 is the product of four consecutive odd of squares of these four odd numbers.

(A) 40000  (B) 40010   (c) 40020

(D) 40030    (E) 40040

Solution

Problem 8 :

The lengths of the sides of the triangle are

x², 22 - x and x - 2

The total number of possible integer value of x is.

(A) 0       (B) 1      (C) 2       (D) 3    (E) 4

Solution

Problem 9 :

Find the value of 

Solution

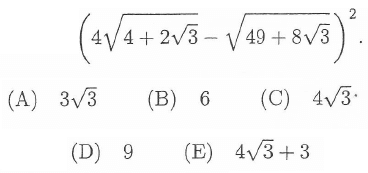
Problem 10 :

If x and y satisfy the equation 2x² + 3y² = 4x, the maximum value of 10x + 6y² is

(A) 2       (B) 9/2      (C) 20       (D) 81/4    (E) None

Solution