SAT Practice Problems on Trigonometry Worksheet
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
sin(x) = cos(K − x)
In the equation above, the angle measures are in radians and K is a constant. Which of the following could be the value of K?
A) 0 B) π/4 C) π/2 D) π
Problem 2 :
In a right triangle, one angle measures x°, where
sin x° = 4/5
What is cos(90° − x°) ?
Problem 3 :
In a circle with center O, central angle AOB has a measure of 5π/4 radians. The area of the sector formed by central angle AOB is what fraction of the area of the circle?
Problem 4 :
In the -xy plane above, O is the center of the circle, and the measure of ∠POQ is kπ radians. What is the value of k?
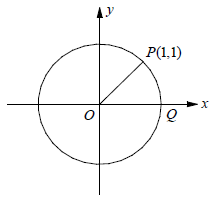
Problem 5 :
In the -xy plane above, O is the center of the circle and the measure of ∠AOD is π/3. If the radius of circle O is 6 what is the length of AD?
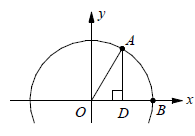
Problem 6 :
Which of the following is equal to cos(π/8) ?
A) cos 3π/8 B) cos 7π/8
C) sin 3π/8 D) sin 7π/8
Problem 7 :
In the figure above, what is the value of cos ∠AOD?
A) 3/5 B) 3/4 C) 4/5 D) 4/3
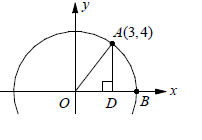
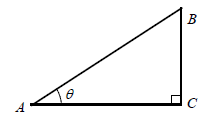
Problem 8 :
In the right triangle shown below, if tan θ = 3/4, what is sin θ?
A) 1/3 B) 1/2 C) 4/5 D) 3/5
Problem 9 :
In the xy-plane above, O is the center of the circle and the measure of ∠POQ is k π radians.
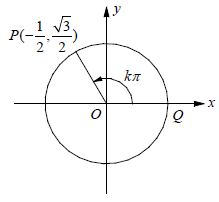
What is the value of k ?
A) 1/3 B) 1/2 C) 2/3 D) 3/4
Problem 10 :
In the right triangle ABC above, the cosine of x° is 3/5. If BC = 12, what is the length of AC?
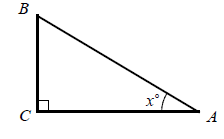
Answer Key
1) k = π/2
2) 4/5
3) area of the sector is 5/8 of area of circle.
4) k = 1/4
5) AD = 3√3
6) sin 3π/8
7) cos θ = 3/5
8) cos θ = 3/5
9) k = 2/3
10) AC = 9
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling