SAT PRACTICE QUESTIONS ON COMPOSITION OF FUNCTION

Problem 1 :

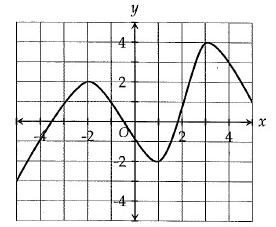
What is the difference between the minimum and maximum values of the function graphed in the xy-plane above, for -5 ≤ x ≤ 5?

Solution:

When x = -5, y is the minimum = -3

When x = 3, y is the minimum = 4

So, the difference is |-3 - 4| = 7 

Problem 2 :

In the xy-plane, the points (a, 7) and (b, 12) lie on the graph of y = x² + 3. What is the minimum possible value of a + b?

A) -5        B) -1     C) 1     D) 5

Solution:

Given, y = x² + 3

7 = a² + 3

a² = 7 - 3

a² = 4

a = 2 or a = -2

12 = b² + 3 

b² = 9

b = 3 or b = -3

Minimum value, a = -2 and b = -3

a + b = -2 - 3 

a + b = -5

So, option (A) is correct.

Problem 3 :

The functions f and g are defined by f(x) = x² + 2 and g(x) = 4x - 3. If a > 0, for what value of a does g(f(a)) = 41?

Solution:

Given, f(x) = x² + 2

f(a) = a² + 2

g(f(a)) = 4(a² + 2) - 3

4a² + 8 - 3 = 41

4a² + 5 - 41 = 0

4a² - 36 = 0

4a² = 36

a² = 36/4

a² = 9

a = ±3

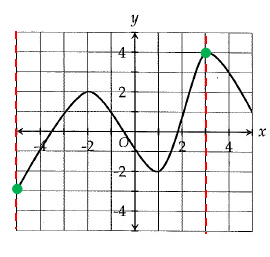
Problem 4 :

The function y = f(x), defined for -3 ≤ x ≤ 4, is graphed in the xy-plane above. Which of the following gives all values of x for which f(x) is negative.

A) -3 ≤ x ≤ 4     B) -2 < x ≤ 4    C) -2 < x < 0 and 3 < x ≤ 4

D) -3 ≤ x < -2 and 0 < x < 3

Solution :

By observing the figure,

• in between -2 and 0, the curve is below the x-axis.
• In between 3 to 4, the curve is below the x-axis.

From this, the output is negative.

So, the answer is -2 < x < 0 and 3 < x ≤ 4

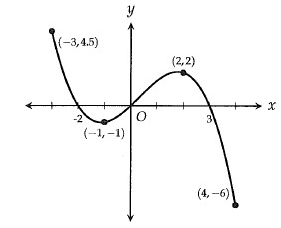
Problem 5 :

The complete function f is shown in the xy-plane above. If f(x) = k has two solutions, which of the following could be the value of k?

I. -3     II. 0    III. 2.5

A) I and II only        B) III only        C) I and III only

D) I, II and III

Solution:

f(x) = k

Drawing the horizontal lines at -3, 0 and 2.5, the horizontal lines intersecting the curve at two different values.

I, II, III, option D is correct.

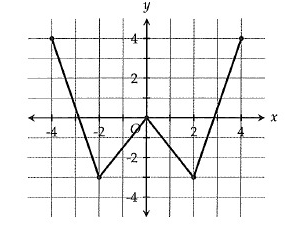
Problem 6 :

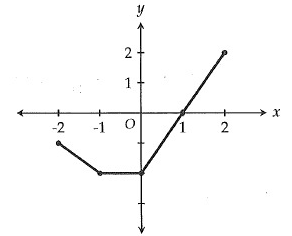
The graph of f(x) is shown in the xy-plane above. If f(a) = -2, which of the following is a possible value of a?

A) -1.5           B) -0.5           C) 1             D) 2

Solution:

According to the graph,

f(x) = -2

y = -2

Drawing the horizontal line through y = -2

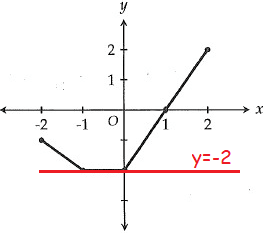
-1 ≤ x ≤ 0

f(-0.5) = -2

So, option (B) is correct.

Problem 7 :

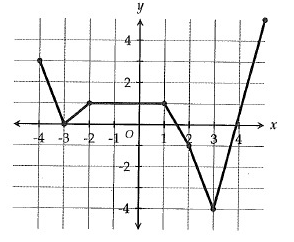
The graph above shows the function g. What is the value of g(3) ?

A) -4      B) 0      C) 3       D) 4

Solution:

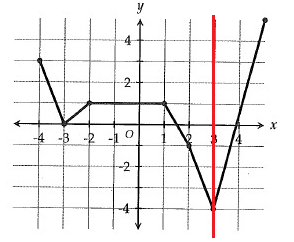
The value of g(3) = -4

So, option (A) is correct.