SAT PRACTICE PROBLEMS ON SPECIAL RIGHT TRIANGLES

Problem 1 :

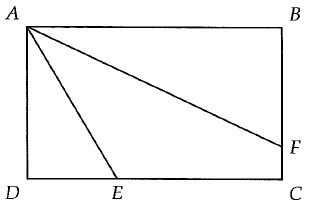
In rectangle ABCD above, E is on DC, F is on BC, DE = 6 and FC = 1. If the angle A is trisected (divided into three equal angles) by AE and AF, what is the length of BF ?

(a)  5     (b) 5√2 - 1     (c) 5√3-1     (d) 6√3-1

Solution :

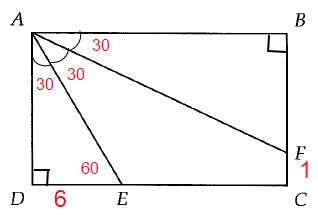
In Δ ADE,

Hypotenuse = AE, Shorter leg = DE = 6 and Longer leg = AD

Hypotenuse = 2(Shorter leg)

Hypotenuse = 2(6)  ==> 12

Longer leg = √3(Shorter leg)

Longer leg = √3(6)

= 6√3

BC = 6√3

BF = BC - FC

BF = 6√3 - 1

So, the length of BF is 6√3 - 1.

Problem 2 :

In triangle ABD above, AB = 10, AC = 6 and CD = 8√3. What is the length of BD ?

Solution :

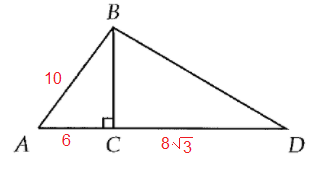
In triangle ABC.

Using Pythagorean theorem :

AB² = AC² + BC²

10² = 6² + BC²

100 - 36 = BC²

BC² = 64

BC = 8

In triangle BCD.

BD² = BC² + CD²

BD² = 8² + (8√3)²

BD² = 64 + 192

BD² = 256

BD = 16

Problem 3 :

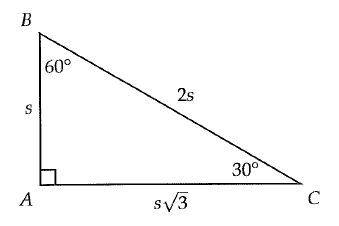
In triangle ABC above, the lengths of the sides relate to one another as shown. If the new triangle is created by increasing s by 40 percent and maintaining the relationships among the sides, the area of the new triangle is how many times greater than the area of the triangle ABC ?

(a)  1.16     (b)  1.96      (c)  1.98       (d)  2.16

Solution :

Area of triangle ABC = (1/2) x base x height

= (1/2) x s√3 x s

= √3 s²/2

The new triangle is created by increasing s by 40%, we get

= (1/2) x 140% of s√3 x 140% of s

= (1/2) x 1.4 s√3 x 1.4 s

= 1.96√3 s²/2

= 1.96(Area of triangle before the changes done)

Problem 4 :

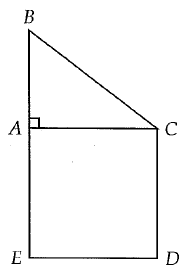
In the figure above, ACDE is square and ABC is a right triangle. If AB = 3 and BC = 5, what is the length of BD ?

(a)  √53     (b)  √62     (c)  8      (d)  √65

Solution :

AB = 3 and BC = 5

BC² = AB² + AC²

5² = 3² + AC²

25 - 9 = AC²

AC² = 16

AC = 4

BD² = BE² + ED²

BD² = (4+3)² + 4²

BD² = 7² + 4²

BD² = 49+16

BD² = 65

BD = √65

Problem 5 :

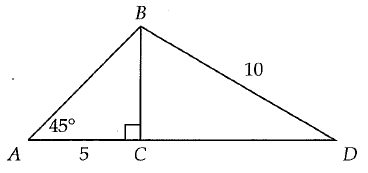
In triangle ABD above, AC = 5 and BD = 10. What is the length of CD ?

Solution :

AC = 5, BC = 5

In triangle BDC,

BD² = BC² + CD²

10² = 5² + CD²

CD² = 100 - 25

CD² = 75

CD = √75

CD = 5√3

So, the length of CD is 5√3.

Problem 6 :

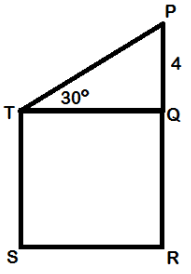
In the figure shown, ΔPQT is a right triangle, and QRST is a square. Find the area of the square, QRST

Solution :

PTQ is right triangle, TQ is perpendicular to PR.

∠TQP = 90

Triangle PTQ is 30-60-90.

Longer leg = TQ, shorter leg = PQ = 4

Hypotenuse = 2 (shorter leg)

= 2(4)

= 8

Longer leg = √3(shorter leg)

= √3(4)

= 4√3

Area of square = Side x side 

= 4√3 x 4√3

= 16(3)

= 48

Problem 7 :

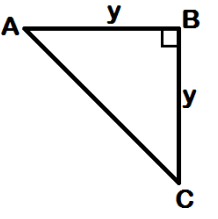
Using the figure above, we are given that the perimeter of ΔABC is 4 + 2√2. Find the value of y.

Solution :

AC² = AB² + BC²

AC² = y² + y²

AC² = 2y²

AC = √(2y²)

AC = y√2

Perimeter of triangle ABC = AB + BC + CA

y√2 + y + y =  4 + 2√2

2y+ y√2 = 4 + 2√2

y(2 + √2) = 2(2 +√2)

y = 2

So, the value of y is 2.

Problem 8 :

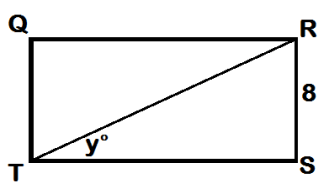
Using the figure above, we are given that QRST is a rectangle, and y = 30º. Find the length of RQ.

Solution :

In Triangle TSR, 30 - 60 - 90

∠RTS = y = 30º

RS = 8 = Shorter leg

Longer leg = TS = RQ

Longer leg = √3(Shorter leg)

= √3 (8)

TS = RQ = 8√3

Problem 9 :

Given a square with diagonal of length 6, calculate the area of the square.

(a) 9      (b)12       (c) 18       (d) 24      (e)  36

Solution :

Length of the diagonal = 6

Side length of square is "x"

x² + x² = 6²

2x² = 36

x² = 18

x = 3√2

Area of the square = 3√2(3√2)

= 9(2)

= 18

Problem 10 :

What is the length of AC.

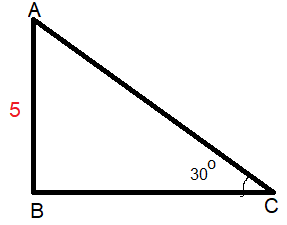
(a) 5√3      (b) 10      (c) 15       (d) 10√3

Solution :

Shorter side = AB = 5

longer side = BC

Hypotenuse = AC = 2(Shorter side)

= 2(5)

AC = 10

Problem 11 :

In the right triangle above x = 60. What is the length of AB?

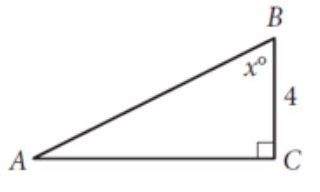
a)  7       b)  8       c)  9      d)  cannot be detemined.

Solution :

∠ABC = 60º (given)

∠ACB = 90º (given)

Then ∠BAC = 30º (given)

In 30-60-90 triangle, AB is hypotenuse. Smaller side = 4

Hypontenuse (AB) = 2 (smaller side)

= 2(4)

= 8

So, option b is correct.