SAT GEOMETRY PRACTICE

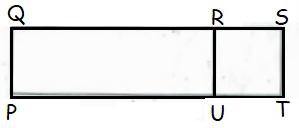
Problem 1 :

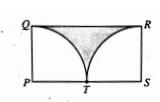
In rectangle PQRS above, arcs QT and RT are quarter circles with centers at P and S, respectively. If the radius of each quarter circle is 1, what is the area of the shaded region?

Solution :

TS and PT are radii of the quadrant. 

PS = 1 + 1 = 2

Length of the rectangle = 2, width of the rectangle = 1

Area of the shaded region = area of rectangle - 2(area of quadrant)

Area of rectangle = 2 x 1 ==> 2 

2 area of quadrant = 2πr²/4

= 2π(1)²/4

= π/2

Area of shaded region = 2 - π/2

Problem 2 :

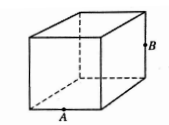
The cube shown above has edges of length 2, and A and B are midpoints of two of the edges. What is the length of AB (not shown) ?

A) √2          B) √3       C) √5          D) √6        E) √10

Solution :

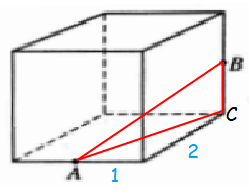
AC² = 1² + 2²

AC² = 5

AC = √5

AB² = AC² + BC²

= (√5)² + 1²

= 5 + 1

AB² = 6

AB = √6

So, option D is correct.

Problem 3 :

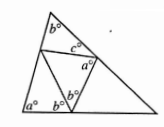
In the figure above, what is the value of c in terms of a and b?

A) a + 3b - 180        B) 2a + 2b - 180       C) 180 - a - b

D) 360 - a - b           E) 360 - 2a - 3b

Solution :

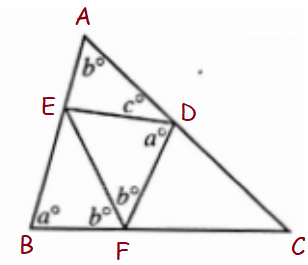
In quadrilateral ADBF,

Sum of interior angles of polygon = (n - 2) x 180

n = 4

= 2(180)

= 360

a + b + b + a + c + b = 360

2a + 3b + c = 360

c = 360 - 2a - 3b

Problem 4 :

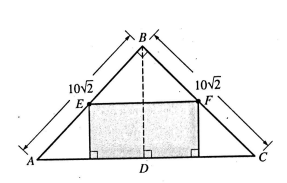
In right triangle ABC above, EF || AC, E and F is the midpoint of BC. What is the area of the shaded rectangular region?

A) 25        B ) 25√2       C) 50    D) 50√2     E) 100

Solution :

Since BE and BF are equal, the triangle BEF must be 45-45-90 right triangle.

EF² = BD² + BF²

EF² = (5√2)² + (5√2)²

EF² = 50 + 50

EF = √100

EF = 10

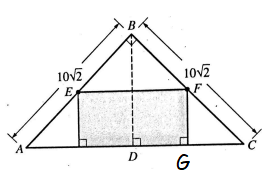
Triangle FGC is 45-45-90 special triangle.

Hypotenuse = √2 (smaller side)

FC = 5√2

GC = 5 = FG

Area of rectangle = length x width

= EF x FG

= 10 x 5

= 50

So, option C is correct.

Problem 5 :

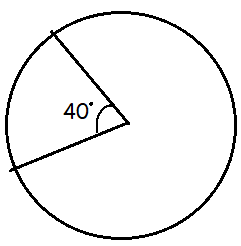
Naomi makes silver jewelry. For one style of earnings she cuts wedges from a silver disk, as shown in the center of the disk. If the weight of each uncut disk is a uniformly distributed 2.5 grams, how many grams does each wedge weigh?

Solution:

Number of wedges with 40 degree can be made = 360/40

= 9 cuts

weight of one uncut disk = 2.5 grams

weight of each wedge = 2.5/9

= 0.27

Approximately 0.3 grams.

Problem 6 :

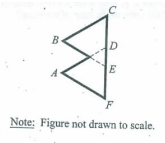
The flag shown is made of overlapping equilateral triangles ADF and BCE. Because ribbon is to be sewn around the entire outer edge, it is necessary to know the perimeter of the flag. If CD, DE, and EF each have length 10 inches, what is the length, in inches, of the perimeter shown in bold?

Solution :

CD = DE = EF = 10 inches

CE = CD + DE ==> 20 inches

The triangle created by the dotted line is also equilateral triangle of side length 10 inches each.

BF = 20 - 10 ==> 10 inches = AF

Perimeter = BC + BG + GA + AF + FE + ED + CD

= 20 + 10 + 10 + 20 + 10 + 10 + 10

= 40 + 50

= 90

Problem 7 :

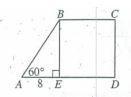
In the figure above, EBCD is a square and AE = 8. What is the area of EBCD?

Solution :

Triangle AEB is a 30-60-90 special right triangle.

AE = smaller side = 8

BE = √3 (smaller side)

BE = 8√3 (side length of square)

Area of BECD = (side length)²

= (8√3)²

= 192 square units.

Problem 8 :

In the figure above, PQST is a rectangle and URST is a square. PU = 5 and UT is a positive integer. If the area of PQST must be more than 10 but less than 30, what is one possible value of UT?

Solution :

Let UT = x, PU = 5, then PT = x + 5

Area of rectangle = length x width

= PT x ST

= (x + 5) x

20 < x (x + 5) < 30

20 < x² + 5x < 30

So, the possible value of x is 3.

Problem 9 :

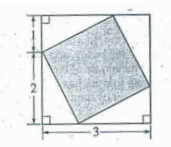
In the figure above, what is the area of the shaded square?

Solution :

Area of one triangle = (1/2) x base x height

= (1/2) x 1 x 2

= 1 square unit

Area of shaded region = Area of square - 4(area of triangle)

= 3 x 3 - 4 (1)

= 9 - 4

= 5 square units.

Problem 10 :

Five points, A, B, C, D, and E, lie on a line, not necessarily in that order. AB has a length of 24. Point C is the midpoint of AB, and point D is the midpoint of AC. If the distance between D and E is 5, what is one possible distance between A and E?

Solution :

AB = 24

C is the midpoint of AB, then AC = CB = 12

D is the midpoint of AC, then AD = 6

DE = 5

AE = AD + DE

= 6 + 5

AE = 11

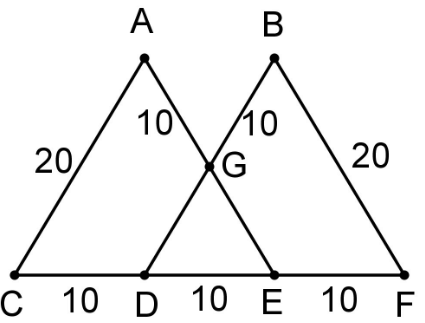
Problem 11 :

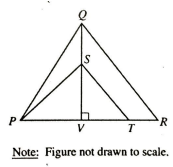
Solution :

If two triangles are similar, then its corresponding side will be proportional.