PSAT MATH QUESTIONS IN ALGEBRA

Problem 1 :

7m = 5(n + p)

The given equation relates the positive numbers m, n, and p. Which equation correctly gives n in terms of m and p ?

Solution :

7m = 5(n + p)

7m = 5n + 5p

5n = 7m - 5p

n = (7/5)m - (5p/5)

n = (7/5)m - p

So, option b is correct.

Problem 2 :

A rectangle has a length that is 15 times its width. The function y = (15 w)(w) represents this situation, where y is the area, in square feet, of the rectangle and y > 0 . Which of the following is the best interpretation of 15w in this context?

A) The length of the rectangle, in feet

B) The area of the rectangle, in square feet

C) The difference between the length and the width of the rectangle, in feet

D) The width of the rectangle, in feet

Solution :

Let we be the width

Then accordingly the given context,

A rectangle has a length that is 15 times its width :

length = 15 w

width = w

Area of rectangle = length x width

= 15w x w

So, 15w is length of the rectangle.

Problem 3 :

x + 2y = 6

x - 2y = 4

The solution to the given system of equations is (x, y). What is the value of x ?

A) 2.5      B) 5      C) 6      D) 10

Solution :

x + 2y = 6 ----(1)

x - y = 4 ----(2)

To solve for x, let us eliminate y.

(1) + (2) ==> x + 2y + x - 2y = 6 + 4

2x = 10

x = 5

Problem 4 :

The table shows the frequency of values in a data set

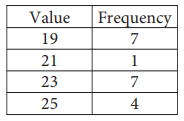
What is the minimum value of the data set?

Solution :

Understanding the table,

The value 19 is repeated 7 times, 21 is repeated 1 time and so on.

By observing it, we understand that 19 is the minimum value.

Problem 5 :

A number x is at most 17 less than 5 times the value of y. If the value of y is 3, what is the greatest possible value of x ?

Solution :

x ≤ 5y - 17

y = 3

x ≤ 5(3) - 17

x ≤ 15 - 17

x ≤ -2

So, the maximum value of x is -2.

Problem 6 :

5x² - 37x - 24 = 0

What is the positive solution to the given equation?

A) 3/5    B) 3     C) 8      D) 37

Solution :

5x² - 37x - 24 = 0

5x² - 40x + 3x - 24 = 0

5x(x - 8) + 3(x - 8) = 0

(5x + 3) (x - 8) = 0

Equating each factor to 0, we get

x = -3/5 and x = 8

So, the positive solution is 8.

Problem 7 :

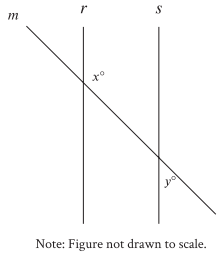
In the figure shown, lines r and s are parallel, and line m intersects both lines. If y < 65 , which of the following must be true?

A) x < 115     B) x > 115    C) x + y < 180     D) x + y > 180

Solution :

Since the lines r and s are parallel, we mark the corresponding angle for x.

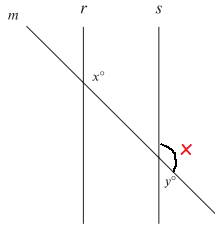
Here x and y are supplementary,

x + y = 180

Since y < 65

If y < 65, then x > 115. Option b is correct.

Problem 8 :

In the given function f, a is a constant. The graph of function f in the xy-plane, where y = f(x) , is translated 3 units down and 4 units to the right to produce the graph of y = g(x). Which equation defines function g ?

Solution :

h and k will represent the horizontal and vertical movement.

h = 4, k = -3

Problem 9 :

A machine launches a softball from ground level. The softball reaches a maximum height of 51.84 meters above the ground at 1.8 seconds and hits the ground at 3.6 seconds. Which equation represents the height above ground h, in meters, of the softball t seconds after it is launched?

A) h(t) = -t² + 3.6                  B) h(t) = -t² + 51.84

C) h(t) = -16(t - 1.8)² - 3.6          D) h(t) = -16(t - 1.8)² + 51.84

Solution :

Considering option D

h(t) = -16(t - 1.8)² + 51.84

y = a(x - h)² + k

Here (h, k) represents the vertex, since the parabola opens down, we can understand that it will have maximum value at (h, k)

h = 1.8 and k = 51.84

The soft ball reaches the ground at 3.6 seconds.

Here h(t) = 0

0 = -16(t - 1.8)² + 51.84

51.84/16 = (t - 1.8)² 

3.24 = (t - 1.8)² 

√3.24 = t - 1.8

1.8 = t - 1.8

t = 1.8 + 1.8

t = 3.6

From this we come to know that it reaches the ground at 3.6 seconds. So, option D is correct.

Problem 10 :

In triangle ABC , the measure of angle B is 90° and BD is an altitude of the triangle. The length of AB is 15 and the length of AC is 23 greater than the length of AB. What is the value of BC/BD ?

A) 15/38     B) 15/23      C) 23/15       D) 38/15

Solution :

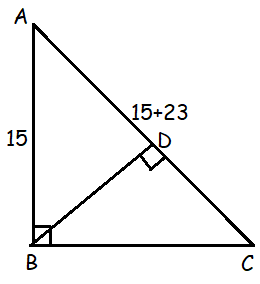
Using the concept of similar triangle. Considering triangle ABC and BDC.

AC/BC = AB/BD

38/BC = 15/BD

38/15 = BC/BD

So, option d is correct.

Problem 11 :

f (x) = (x + 7)² + 4

The function f is defined by the given equation. For what value of x does f (x) reach its minimum?

Solution :

Comparing the given function f(x) with

y = a(x - h)² + k

Sign of a is positive, so the parabola opens up. Then it will have minimum value.

(h, k) is (-7, 4)

The minimum value is 4 when x = -7