PSAT MATH QUESTIONS ALGEBRA

Problem 1 :

How many teaspoons are equivalent to 44 tablespoons?

(3 teaspoons = 1 tablespoon)

A) 47     B) 88      C) 132         D) 176

Solution :

3 teaspoons = 1 tablespoon

44 tablespoons = 3 x 44

= 132 teaspoons

Problem 2 :

The function f is defined by f(x) = 1/6x . What is the value of f (x) when x = 3 ?

A) 1/3      B) 1/6      C) 1/9      D) 1/18

Solution :

f(x) = 1/6x

When x = 3

f(3) = 1/6(3)

= 1/18

Problem 3 :

If x = 40 , what is the value of x + 6 ?

A) 34     B) 40      C) 46      D) 64

Solution :

Let y = x + 6

Applying x = 40, we get

y = 40 + 6

= 46

Problem 4 :

What is 23% of 100?

A) 23     B) 46     C) 77     D) 123

Solution :

= 23% of 100

= 0.23 x 100

= 23

Problem 5 :

Which expression is equivalent to 50x² + 5x²?

A) 250x²     B) 10x²    C) 45x²    D) 55x²

Solution :

50x² + 5x²

Adding the like terms, we get

= 55x²

Problem 6 :

The population density of Cedar County is 230 people per square mile. The county has a population of 85,100 people. What is the area, in square miles, of Cedar County?

Solution :

Let x be the number of square miles required.

1 : 230 people = x : 85100

85100 = 230x

x = 85100/230

x = 370

So, the required number of square miles is 370.

Problem 7 :

-54/w = 6

What is the solution to the given equation ?

Solution :

-54/w = 6

Multiplying by w on both sides, we get

-54 = 6w

Dividing by 6 on both sides.

-54/6 = w

w = -9

Problem 8 :

For the function f, the graph of y = f(x) in the xy-plane has a slope of 3 and passes through the point (0, −8) . Which equation defines f ?

A) f(x)  = 3x    B)  f(x) = 3x - 8        C)  f(x) = 3x + 5

D)  f(x) = 3x + 11

Solution :

Equation of the line passes through the point (0, -8) and having slope of 3.

y - y₁ = m(x - x₁)

y - (-8) = 3(x - 0)

y + 8 = 3x

y = 3x - 8

f(x) = 3x - 8

Problem 9 :

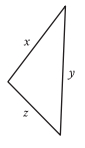
The triangle shown has a perimeter of 22 units. If x = 9 units and y = 7 units, what is the value of z, in units?

A) 6        B) 7      C) 9       D) 16

Solution :

x = 9 units and y = 7 units

Perimeter of the triangle = 22 units

x + y + z = 22

9 + 7 + z = 22

z + 16 = 22

z = 22 - 16

z = 6 units.

Problem 10 :

The function h is defined by h(x) = 3x − 7 . What is the value of h(−2) ?

A) −13     B) −10      C) 10      D) 13

Solution :

h(x) = 3x − 7

Applying -2 as x.

h(-2) = 3(-2) - 7

= -6 - 7

= -13

Problem 11 :

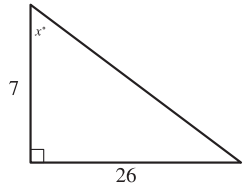
In the triangle shown, what is the value of tan ° x ?

A) 1/26    B) 19/26     C) 26/7     D) 33/7

Solution :

Side opposite to 90 degree = hypotenuse

Side opposite to x = opposite side = 26

Adjacent side = 7

tan x = opposite side / adjacent side

tan x = 26/7

Problem 12 :

The scatterplot shows the relationship between x and y. A line of best fit is also shown.

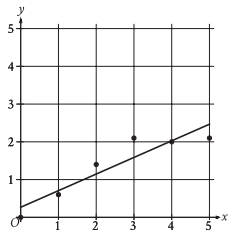
Which of the following is closest to the slope of the line of best fit shown?

A) −2.27      B) −0.44     C) 0.44     D) 2.27

Solution :

Choosing two points which are closer to the line, we get

(1, 0.7) and (4, 2)

slope of the line = (y2 - y1) / (x2 - x1)

= (2 - 0.7) / (4 - 1)

= 1.3/3

= 0.44

Since the line of best fit is a raising line, we will get positive slope, so we can ignore option A and B.

Problem 13 :

The y-intercept of the graph of 12x + 2y = 18 in the xy-plane is (0, y) . What is the value of y ?

Solution :

12x + 2y = 18

y-intercept :

Put x = 0

12(0) + 2y = 18

2y = 18

y = 9

Problem 14 :

A model predicts that a certain animal weighed 241 pounds when it was born and that the animal gained 3 pounds per day in its first year of life. This model is defined by an equation in the form f(x) = a + bx, where f (x) is the predicted weight, in pounds, of the animal x days after it was born, and a and are constants. What is the value of a ?

Solution :

f(x) = a + bx

Here a is y-intercept and b is slope.

Weight of animal = 241 pounds

Rate of change = slope = 3 pounds per day

a = 241

Problem 15 : 

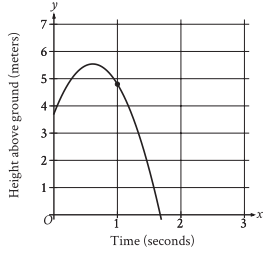
The graph shows the height above ground, in meters, of a ball x seconds after the ball was launched upward from a platform. Which statement is the best interpretation of the marked point (1.0, 4.8) in this context?

A) 1.0 second after being launched, the ball’s height above ground is 4.8 meters.

B) 4.8 seconds after being launched, the ball’s height above ground is 1.0 meter.

C) The ball was launched from an initial height of 1.0 meter with an initial velocity of 4.8 meters per second.

D) The ball was launched from an initial height of 4.8 meters with an initial velocity of 1.0 meter per second.

Solution :

x = time

y = height above the ground

1.0 second after being launched, the ball’s height above ground is 4.8 meters.

Problem 16 :

Based on a random sample from a population, a researcher estimated that the mean value of a certain variable for the population is 20.5, with an associated margin of error of 1. Which of the following is the most appropriate conclusion?

A) It is plausible that the actual mean value of the variable for the population is between 19.5 and 21.5.

B) It is not possible that the mean value of the variable for the population is less than 19.5 or greater than 21.5.

C) Every value of the variable in the population is between 19.5 and 21.5.

D) The mean value of the variable for the population is 20.5.

Solution :

Estimated mean = 20.5

Marginal error = 1

20.5 - 1 ==> 19.5

20.5 + 1 ==> 21.5

So, option A is correct.