PSAT MATH PRACTICE TEST

Problem 1 :

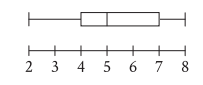
The box plot summarizes 15 data values. What is the median of this data set?

A) 2     B) 3     C) 5     D) 8

Solution :

Median is 5.

Problem 2 :

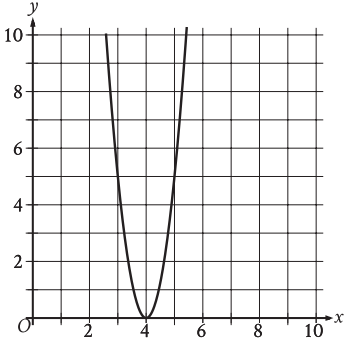
What is the x-intercept of the graph shown?

A) (−5, 0)       B) (5, 0)       C) (−4, 0)        D) (4, 0)

Solution :

By observing the graph, the parabola touches the x-axis at 4.

So, the x-intercepts are (4, 0) and (4, 0).

Problem 3 :

Henry receives a $60.00 gift card to pay for movies online. He uses his gift card to buy 3 movies for $7.50 each. If he spends the rest of his gift card balance on renting movies for $1.50 each, how many movies can Henry rent?

A) 10      B) 25       C) 35      D) 40

Solution :

Number of movies he is busying = 3

Cost of each movie = $7.50

Cost spent for movies = 3(7.50)

= 22.5

Remaining money = 60 - 22.5

= 37.5

Number of movies renting = x

1.5x = 37.5

x = 37.5/1.5

x = 25

Problem 4 :

x = 49

y = √x+9

The graphs of the given equations intersect at the point (x, y) in the xy-plane. What is the value of y ?

A) 16     B) 40     C) 81     D) 130

Solution :

x = 49 ----(1)

y = √x+9 ----(2)

Applying the value of x in (2), we get

y = √49 + 9

= 7 + 9

= 16

So, the value of y is 16.

Problem 5 :

If 2x = 12, what is the value of 9x ?

Solution :

2x = 12

Dividing by 2 on both sides

x = 12/2

x = 6

Problem 6 :

Line k is defined by

y = (1/4)x + 1

Line j is parallel to line k in the xy-plane. What is the slope of j ?

Solution :

If two lines are parallel, then slopes will be equal.

y = (1/4)x + 1

Comparing with y = mx + b

Slope (m) = 1/4

Problem 7 :

6, 6, 8, 8, 8, 10, 21

Which of the following lists represents a data set that has the same median as the data set shown?

A) 4, 6, 6, 6, 8, 8       B) 6, 6, 8, 8, 10, 10

C) 6, 8, 10, 10, 10, 12      D) 8, 8, 10, 10, 21, 21

Solution :

6, 6, 8, 8, 8, 10, 21

The given data is arranged in ascending order.

Number of elements = 7

median = 8

So, option B is correct.

Problem 8 :

The length of the base of a certain parallelogram is 89% of the height of the parallelogram. Which expression represents the length of the base of the parallelogram, where h is the height of the parallelogram?

A) 89h      B) 0.089h     C) 8.9h        D) 0.89h

Solution :

Let b be the base of the parallelogram and h be the height.

base = 89% of h

= 0.89 h

So, option D is correct.

Problem 9 :

For a camping trip a group bought x one-liter bottles of water and y three-liter bottles of water, for a total of 240 liters of water. Which equation represents this situation?

A) x + 3y = 240        B) x + y = 240

C) 3x + 3y = 240     D) 3x + y = 240

Solution :

x be the number of 1 liter bottle and y be the number of 3 liter bottle.

Quantity of water bottle = 240

1x + 3y = 240

So, option A is correct.

Problem 10 :

y = −4x + 40

Which table gives three values of x and their corresponding values of y for the given equation?

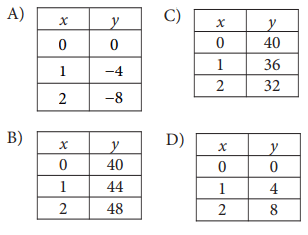
Solution :

So, option B is correct.

Problem 11 :

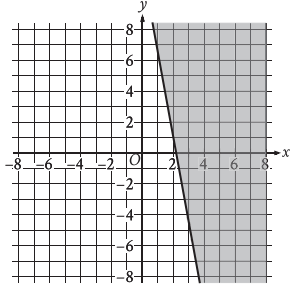
The shaded region shown represents solutions to an inequality. Which ordered pair (x, y) is a solution to this inequality?

A) (0, −4)    B) (0, 4)      C) (−4, 0)      D) (4, 0)

Solution :

(4, 0) is one of the point on the shaded region. So, option D is correct.

Problem 12 :

In triangle JKL , the measures of ∠K and ∠L are each 48°. What is the measure of ∠J, in degrees? (Disregard the degree symbol when entering your answer.)

Solution :

Sum of interior angles of triangle = 180°

∠J + ∠K + ∠L = 180°

∠J + 48 + 48 = 180°

∠J + 96 = 180°

∠J = 180° - 96°

∠J = 84°

Problem 13 :

y = x² + 14x + 48

x + 8 = 11

The solution to the given system of equations is (x, y). What is the value of y ?

Solution :

y = x² + 14x + 48 -----(1)

x + 8 = 11-----(2)

x = 11 - 8

x = 3

Applying the value of x in (1), we get

y = 3² + 14(3) + 48

y = 9 + 42 + 48

y = 99

So, the value of y is 99.

Problem 14 :

A cleaning service that cleans both offices and homes can clean at most 14 places per day. Which inequality represents this situation, where f is the number of offices and h is the number of homes?

A) f + h ≤ 14      B) f + h ≥ 14       C) f - h ≤ 14      D) f - h ≥ 14

Solution :

At most 14 places, which means ≤ 14.

f is the number of offices and h is the number of homes

f + h ≤ 14.

Problem 15 :

Which expression is a factor of

2x² + 38x + 10 ?

A) 2      B) 5x     C) 38x    D) 2x²

Solution :

= 2x² + 38x + 10

= 2(x² + 19x + 5)

So, the common factor is 2.