NC MATH 3 PRACTICE QUESTIONS

Write the inverse for each equation and find the following.

i) Check whether the inverse is a function or not.

ii) Find domain and range.

Problem 1 :

y = -(3/5)x - 12

Solution :

To find inverse of any function, we have to follow the steps given below.

Step 1 :

y = -(3/5)x - 12

Solving for x

y = -(3/5)x - 12

y + 12 = -(3/5)x

x = (-5/3) (y + 12)

Step 2 :

Change x as f^-1(x) and y as x.

f^-1(x) = (-5/3) (x + 12)

By applying some random values of x, we get different values of y. Hence inverse function is also a function.

Domain :

Since the given function is linear, all real values are domain.

So, domain is (-∞, ∞).

Range :

(-∞, ∞)

Problem 2 :

y = √x - 5 + 8

Solution :

Finding inverse function.

Step 1 :

y = √x - 5 + 8

Solving for x

y - 8 = √x - 5

(y - 8)² = x - 5

x = (y - 8)² + 5

x - 5 = (y - 8)²

y - 8 = √(x - 5)

y = √(x - 5) + 8

Step 2 :

Change x as f^-1(x) and y as x.

f^-1(x) =√(x - 5) + 8

By applying some random values of x, we get different values of y. Hence inverse function is also a function.

Domain :

Since it is square root function, the value which is inside the radical should be greater than or equal to 0.

(x - 5) ≥ 0

x ≥ 5

Range :

(-∞, ∞)

Problem 3 :

Which of the following expression is having the factor of x - 2.

a)  3x³ + 6x² - 6x - 36         b) 2x³ + 5x² - x - 6

c)  x⁴ + 3x³ - 10x²      d)  3x⁴ + 2x² - 35x² - 18x + 72

Solution :

Option a :

3x³ + 6x² - 6x - 36

Factoring 3, we get 

= 3(x³ + 2x² - 2x - 12)

Using the method of grouping finding factors, we get

= 3x² ((x + 2) - 2(x + 6))

It is not factorable using the method of grouping. Then option a is not correct.

Option c :

= x⁴ + 3x³ - 10x²

= x²(x² + 3x - 10)

= x²(x² + 5x - 2x - 10)

= x²[x (x + 5) - 2 (x + 5)]

= x²(x - 2) (x + 5)

So, option c is correct.

Problem 4 :

Nancy can paint a fence in 3 hours. It takes Ben 4 hours to do the same job. If they were to work together to paint a fence, approximately how many hours should it take?

A. 1.7     B. 2.0     C. 3.2      D. 5.8

Solution :

Time taken by Nancy to complete the work = 3 hours

Time taken by Ben to complete the work = 4 hours

1/3 be the work done by Nancy in 1 hour.

1/4 be the work done by Ben in 1 hour.

= 1/3 + 1/4

= (4 + 3)/12

= 7/12

time taken to complete the work = 12/7

= 1.71

So, option a is correct.

Problem 5 :

In the diagram below of circle O, chords and intersect at E.

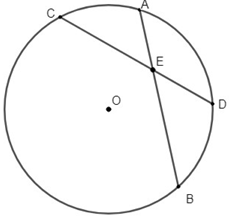
If CE = 10, ED = 6 and AE = 4, what is the length of EB

A. 2.4    B. 6.7     C. 12     D. 15

Solution :

When chords intersect inside the circle, the product of two parts of the chords are equal

CE ⋅ ED = AE ⋅ EB

10 ⋅ 6 = 4 ⋅ EB

EB = 60/4

EB = 15

so, option D is correct.

Problem 6 :

A polynomial equation with real coefficients has roots at x = ±1 and x = 2i. What is the minimum degree of the polynomial equation?

A. 3    B. 4     C. 5     D. 6

Solution :

If the given root is a rational or it is complex number, then its conjugate will be other root.

Hence the roots are x = 1, x = -1, x = 2i and x = -2i. Then, the polynomial which is having the highest exponent is 4.

Problem 7 :

In the figure below, the larger circle has a radius of 6 cm and the smaller circle has a radius of 2 cm.

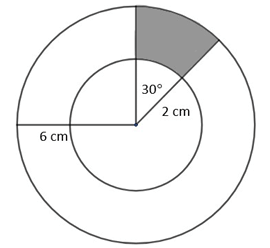
What is the approximate area of the shaded region?

A. 2.1 cm²   B. 3.4 cm²   C. 4.2 cm²   D. 8.4 cm²

Solution :

Area of shaded portion = area of large sector - area of small sector

= (θ/360) πR² -  (θ/360) πr²

= (θ/360) π(R² - r²)

= (30/360) x 3.14 (6² - 2²)

= (1/12) x 3.14 (36-4)

= (1/12) x 3.14 x 32

= 8.37 

Approximately 8.4 cm². So, option D is correct.

Problem 8 :

Factor the expression.

x³ - 5x² + 3x - 15

Solution :

= x³ - 5x² + 3x - 15

Factor x², we get

= x² (x - 5) + 3(x - 5)

= (x² + 3) (x - 5)

So, the factors are (x² + 3) (x - 5).