GL MATHS ASSESSMENT PAPERS ONLINE

Problem 31 :

Henry and John started walking from the same point. Henry went 1 km north, 2 km west, 4 km south and 1 km west. John went 1 km east, 4 km south and 4 km west. Which of the following must be the final part of his walk in order to reach the same point as Henry?

a) He has already reached      b) 1 km north

c) More than 1 km north west    d) 1 km west

Solution :

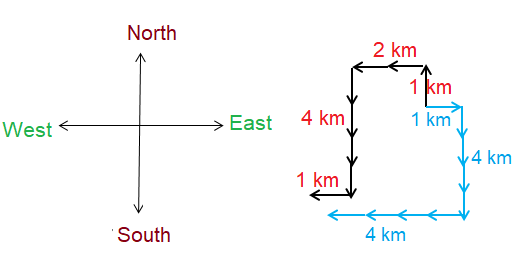
So, the answer is 1 km north.

Problem 32 :

The natural number has three digits. When we multiply the digits we get 135. What result do we get, if we add the digits?

a) 14     b) 15   c) 16     d)  17

Solution :

Decomposing 135 into prime factors,

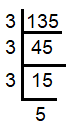
135 = 3 x 3 x 3 x 5

The three numbers involving in this problem are not consecutive numbers.

3 x 9 x 5 = 135 and sum of 3, 9 and 5 is 14.

Problem 33 :

In a restaurant, there are 16 tables each having 3, 4 or 6 chairs. Together the table having 3 or 4 chairs can accommodate 36 people. Knowing that the restaurant can accommodate 72 people. How many tables are there with 3 chairs?

a) 4    b) 5      c) 6     d)  7

Solution :

36 people can accommodate having 3 or 4 chairs.

Remaining 36 can accommodate 6 chairs.

Let x and y be the number of chairs having 3 seats and 4 seats respectively.

3x + 4y = 36 ----(1)

x + y = 16 - 6

x + y = 10 

y = 10 - x

3x + 4(10 - x) = 36

3x + 40 - 4x = 36

-x = -4

x = 4

Applying x = 4 in y = 10 - x, then y = 6

So, the number of tables having 3 seats is 4.

Problem 34 :

Three people are going round in a circular field of 360 km circumference. They can travel 48 km, 60 km and 72 km in a day respectively. When will they meet?

a) 25 days    b) 720 days    c) 360 days    d)  30 days

Solution :

Let A, B and C be three persons.

Time taken to cover 360 km by A = 360 / 48 ==> 7.5 days

Time taken to cover 360 km by B = 360 / 60 ==> 6 days

Time taken to cover 360 km by C = 360 / 72 ==> 5 days

LCM of 7.5, 6 and 5

Multiplying each quantity by 10, we get

75, 60 and 50

lcm = 5 x 5 x 3 x 2 x 2

= 300

Dividing by 10, we get 30. So, the answer is 30 days.

Problem 35 :

A cake weighs 900g. Paul cut it into 4 pieces. The biggest piece is as heavy as other weights altogether. What is the weight of biggest piece?

a) 150g        b) 450g          c) 350g          d)  100g

Solution :

Let x be the weight of 1 piece, then 3x be the weight of other pieces.

3 small pieces + 1 large piece = 900

x + x + x + 3x = 900

6x = 900

x = 900/6

x = 150

weight of large piece = 3(150) = 450

Problem 36 :

Jenny had a pizza that was divided into 8 equal slices. She ate 3 of them. Danny has a pizza that is the same size but was divided into 4 equal slices. He ate 3 slices of his pizza. Who ate more pizza?

a) Jenny    b) Danny     c) Both      d) No one

Solution :

Jenny ate 3/8 part of pizza

Danny ate 3/4 part of pizza

Converting 3/4 with the denominator of 8, we get

6/8 > 3/8

So, Danny ate more.

Problem 37 :

How many pairs of adjacent angles does a quadrilateral have?

a) Two    b) Three    c) Four    d)  six

Solution :

There are four pairs of adjacent angles.

Problem 38 :

A square of perimeter 48 cm is cut into 2 equal pieces to make rectangle. What is the perimeter of the rectangle

a) 36 cm    b) 60 cm    c) 56 cm    d) 96 cm

Solution :

Perimeter of the square = 48 cm

4a = 48

a = 48/4

a = 12

Side length of the square = 12

Width of the rectangle = 12 cm, length = 6 cm

Perimeter = 2 (12 + 6)

= 2(18)

= 36 cm

Problem 39 :

Trees grow on only side of Park Avenue. There are 60 trees in total. Every second tree is a maple, and every third tree is either a Linden or a maple. The remaining trees are birches. How many birches are there?

a) 30    b) 20    c) 10    d)  50

Solution :

By numbering trees, numbers marked as birches are

Every 2nd tree is maple = 60/2 ==> 30 maple trees

Every 3rd tree is either linden or a maple :

= 30/3 ==> 10 Linden or a maple

remaining trees = 60 - 30 - 10

= 20 trees.

Problem 40 :

Grandmother celebrating her birthday today. Sum of her age, daughter’s age and granddaughter’s age is 100. Each of their ages is power of 2. How old is her granddaughter now?

a) 32    b) 16    c) 4    d)  64

Solution :

2^x + 2^y + 2^z = 100

x < y < z

2² = 4, 2³ = 8, 2⁴ = 16, 2⁵ = 32

If we choose 4 and 8 as daughter's age and mother's age respectively. it is not meaningful.

• Choosing 16 and 32 is meaningful, but the remaining 100 - (16+32) cannot be written with the power of 2.
• The combination of 8 and 32, the remaining 60 also cannot be written with the power of 2.
• 64, 32, 4 will give the sum of 100.

So, the age of granddaughter is 4.

Problem 41 :

The measure of an angle is ¾ of 60. What is the measure of its complementary angle?

a) 45    b) 60    c) 120    d)  90

Solution :

The measure of an angle = 3/4 of 60.

= 45

Its complementary angle = 90 - 45

Problem 42 :

The product of two numbers is 1296. If one number is 16 times the other then find the smaller number.

a) 9    b) 81    c) 36    d)  100

Solution :

Let x and y be two numbers.

xy = 1296

x = 16y

16y(y) = 1296

y² = 1296/16

y² = 81

y = 9

x = 16(9)

x = 144

So, the smallest number is 9.

Problem 43 :

A bus can seat 82 people. 8770 people travel to a football match by bus. How many buses are needed?

a)    107   b) 110    c) 106    d) 105

Solution :

Number of seats = 82

Number of people = 8770

Number of buses = 8770/82

= 106.9

= 107

Total buses needed is 107.

Problem 44 :

What is the largest number of 15cm by 30cm by 20cm shoe boxes that can fit in a 1m by 3m by 2m crate?

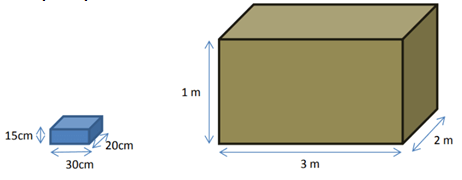
a)    660     b) 666    c) 667   d) 670

Solution :

Number of shoe boxes = (100 x 300 x 200)/(30 x 20 x 15)

= 666.6

= 667