EOC MATH 1 WORKSHEET WITH SOLUTIONS

Problem 1 :

For the given expression, (x - 1)(x - 3) - 5x, simplify to standard form ax² + bx + c, what is a, b and c ?

Solution :

= (x - 1)(x - 3) - 5x

= x² - 3x - x + 3 - 5x

= x² - 4x - 5x + 3

= x² - 9x + 3

Comparing with ax² + bx + c

a = 1, b = -9 and c = 3

Problem 2 :

Given f(x) = x + 4, g(x) = x² - 3x + 5 and h(x) = 3^x + x

a) What is f(x) + g(x) ?

b)  what is f(2) x g(2) ?

c)  what is h(3) ?

Solution :

a) f(x) = x + 4, g(x) = x² - 3x + 5

f(x) + g(x) = x + 4 + x² - 3x + 5

= x² - 2x + 9

b)   f(2) x g(2)

f(2) = 2 + 4 ==> 6

g(2) = 2² - 3(2) + 5

= 4 - 6 + 5

= 9 - 6

= 3

f(2) x g(2) = 6 x 3 ==> 18

c)  h(3) = 3³ + 3

= 27 + 3

h(3) = 30

Problem 3 :

What is the vertex of x² - 10x + 9 ? What quadrant is it in ?

Solution :

Vertex :

x - coordinate = -b/2a

a = 1, b = -10 and c = 9

x = -(-10)/2(1)

x = 10/2

x = 5

Applying the value of x in given quadratic function, we get

y = x² - 10x + 9

y = 5² - 10(5) + 9

y = 25 - 50 + 9

y = -16

Vertex is (5, -16) and it lies in 4^th quadrant.

Problem 4 :

Given the equations : y = 10(1.02)^x and y = 2x + 10

a) What is the rate of the exponential function ?

b) What is the starting point of the exponential function ?

c) Is the exponential function growth or decay ? why ?

d) Which function is steeper ? and why ?

Solution :

y = 10(1.02)^x

Expressing the given function in the form of

y = a(1+r%)^x or y = a(1-r%)^x

y = 10(1 + 2%)^x

So, the given function is growth function

b) To find the starting point, we have to put x = 0

y = 10

c) Since the given function is expressed in the form of 

y = a(1+r%)^x

it is exponential growth function.

d)  The first function is exponential and the second function is linear function. Always exponential function will be steeper then linear function.

Problem 5 :

What is the starting value in the equation y = 3(0.92)^x ?

a) What is the rate ?

b) What is the starting point ?

c) Is it growth or decay, why ?

Solution :

a)  y = 3(0.92)^x

y = a(1-r%)^x

1 - r% = 0.92

1 - 0.92 = r%

0.08 = r%

8% = r%

Rate is 8%.

b)  To find starting point, we apply x = 0

y = 3

c) It is a decay function, the given function is in the form of

y = a(1-r%)^x

Problem 6 :

a. Given the system 2x + 3y = 13 and x = 5y, what is x + y ?

b. Which quadrant does this solution lie ?

Solution :

2x + 3y = 13 -----(1)

x = 5y -----(2)

a)

Applying the value of x in the (1) equation

Solution is (5, 1).

b) The point (5, 1) lies in the 1st quadrant.

Problem 7 :

Given f(x) = x² + 20x - 18 and g(x) = 20x + 18, what is the smallest solution to f(x) = g(x) ?

Solution :

f(x) = x² + 20x - 18 and g(x) = 20x + 18

x² + 20x - 18 = 20x + 18

x² - 18 = 18

x² = 36

x = ±6

Problem 8 :

Let y = 2x -10

a. If m is the x-intercept and n is the y-intercept, what is m - n?

b. If m is the x-intercept and n is the slope, what is m subtracted from n ?

Solution :

a) m - n = 5 - (-10) ==>  15

b)  m = 5, slope (n) = 2

n - m = 2 - 5 ==> -3

Problem 9 :

If f(x) = 3x - p and f(5) = 10, what is the value of p ?

Solution :

f(x) = 3x - p and f(5) = 10

f(5) = 3(5) - p

10 = 15 - p

p = 15 - 10

p = 5

Problem 10 :

Given ((x²)³)⁴ and the expression, x^r what is r ?

Solution :

((x²)³)⁴ = x²⁴

So, the value of r is 24.

Problem 11 :

Simplify 

Solution :

Problem 12 :

Simplify x

Solution :

Problem 13 :

Given the box and whisker plot, what is IQR (interquartile range) and median.

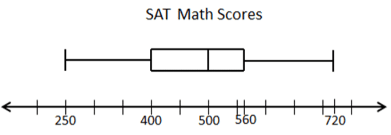
Solution :

Inter quartile range = Q₃ - Q₁

= 560 - 400

= 160

Median = 500

Problem 14 :

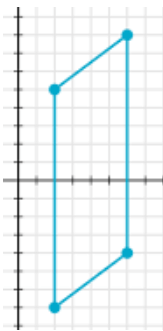
a. What is the area of the parallelogram ?

b. What is the perimeter of the parallelogram ?

Solution :

a)

Base = 12, height = 4

Area of parallelogram = base x height 

= 12 x 4

= 48 square units.

b) Length = 12

To find the width of the parallelogram, we use the picture given 

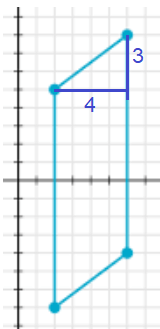
Pythagorean theorem :

w² = 4² + 3²

w² = 16 + 9

w = √25

width = 5

Perimeter of the parallelogram = 2(12 + 5)

= 2(17)

= 34 units

Problem 15 :

a. Does this set of points (1, 2) and (3, 4) make up a line parallel to y = 4 + 3x, why or why not ?

b. Tell the slope of the line perpendicular to y = 4 + 3x

Solution :

Slope of the line passes through the two points (1, 2) and (3, 4)

slope (m) = (4 - 2) / (3 - 1)

= 2/2

= 1

Slope of the given line :

m = 3

Since the slopes are not equal, the lines are not parallel.

b. The product of the slopes is not equal, they are not perpendicular.

Problem 16 :

What is the distance between the solutions for

f(x) = x² + 14x + 49 and g(x) = 4x + 4 ?

Solution :

f(x) = x² + 14x + 49

x² + 14x + 49 = 0

(x + 7)(x + 7) = 0

x = -7 and -7

g(x) = 4x + 4

4x + 4 = 0

4x = -4

x = -1

Distance between -1 and -7 is 6.