AP CALCULUS PRACTICE PROBLEMS ON DERIVATIVE

Problem 1 :

For what value of x does the function

f(x) = x³ - 9x² - 120x + 6

have a local minimum ?

A)  10     B)  4      C)  -4    D)  -10

Solution :

To find at which value of x, the function f(x) has local minimum. Let us find the critical number and draw the sign diagram.

f(x) = x³ - 9x² - 120x + 6

f'(x) = 3x² - 9(2x) - 120(1)

f'(x) = 3x² - 18x - 120

f'(x) = 0

3x² - 18x - 120 = 0

x² - 6x - 40 = 0

(x - 10) (x + 4) = 0

x = 10 and -4

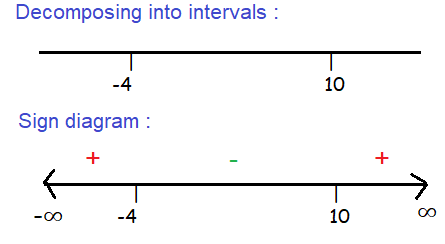
Local minimum :

Slopes decreases ---> increases

negative ---> positive

So, local minimum is at x = 10, option A is correct.

Local maximum :

Slopes increases ---> Decreases

positive ---> negative

So, local maximum is at x = -4.

Problem 2 :

Suppose f'(x) = x (x - 2)² (x + 3). which of the following is (are) true ?

I. f has a local maximum at x = -3

II. f has local minimum at x = 0

III. f has neither a local maximum nor local minimum at x = 2

A)  I only     B)  II only     C)  III only     D) I and II only

E)  I, II and III

Solution :

Finding critical numbers :

f'(x) = x (x - 2)² (x + 3)

f'(x) = 0

x (x - 2)² (x + 3) = 0

x = 0, x = 2 and x = -3

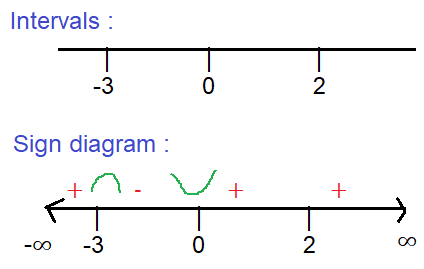
I. f has a local maximum at x = -3

Slopes increases ----> decreases

So, maximum is there at x = -3

II. f has local minimum at x = 0

Slopes decreases ----> Increases

So, minimum is there at x = 0

III. f has neither a local maximum nor local minimum at x = 2

There is no changes in slope, so no maximum or minimum.

Option E is correct.

Problem 3 :

The maximum value of the function 

f(x) = x⁴ - 4x³ + 6 on [1, 4] is 

A)  1      B)  0      C)  3     D)  6      E)  -27

Solution :

f(x) = x⁴ - 4x³ + 6

f'(x) = 4x³ - 12x² + 0

f'(x) = 4x²(x - 3) = 0 

x = 0 (touches) and x = 3(crosses)

Since the interval is given, we find absolute maximum.

x = 1, f(1) = 1⁴ - 4(1)³ + 6 ==> 3 ==> (1, 3)

x = 3, f(3) = 3⁴ - 4(3)³ + 6 ==> -21 ==> (3, -21)

x = 4, f(4) = 4⁴ - 4(4)³ + 6 ==> 6 ==> (4, 6)

So, the maximum value is 6, option D is correct.

Problem 4 :

Find all critical numbers of the function g(x) = x⁴ - 4x²

Solution :

g(x) = x⁴ - 4x²

g'(x) = 4x³ - 4(2x)

= 4x³ - 8x

= 4x(x² - 8)

g'(x) = 0

4x(x² - 8) = 0

x = 0 and x² - 8 = 0

x² = 8

x² = √8

x = 2√2

So, the critical numbers are x = 0, 2√2 and -2√2.

Problem 5 :

Locate the absolute extrema of the function

f(x) = x³ - 12x

on the closed interval [0, 4]

A) absolute max (2, -16) and absolute min (4, 16)

B)  no absolute max, absolute min (4, 16)

C)  absolute max (4,16); absolute min (2, -16)

D) Absolute max (4, 16), no absolute min

E) no absolute max or min.

Solution :

f(x) = x³ - 12x

f'(x) = 3x² - 12(1)

= 3(x² - 4)

= 3(x + 2)(x - 2)

f'(x) = 0

3(x + 2)(x - 2) = 0

x = -2, x = 2

x = 0, f(0) = 0³ - 12(0) ==> 0

x = -2, f(2) = (-2)³ - 12(-2) ==> 16

x = 2, f(2) = 2³ - 12(2) ==> -16 (min)

x = 4, f(4) = 4³ - 12(4) ==> 16 (max)

Absolute maximum is at (4, 16) and absolute minimum is at (2, -16).