8th GRADE MATH EOG PRACTICE TEST

Problem 1 :

A deck has a length 4 feet greater than its width, w. Garrett would like to increase both dimensions of the deck by 2 feet. Which equation represents the new perimeter of the deck ?

A)  P(w)  = 4 w + 8      B)  p(w) = 2w + 4      C) p(w) = 4w + 16

D)  p(w) = 8w + 16

Solution :

Width of the rectangle = w

length of the rectangle = w + 4

length and width both increased by 2.

So, new length = w + 4 +2, new width = w + 2

Perimeter = 2(w + 6 + w + 2)

= 2(2w + 8)

= 2(2)(w + 4)

= 4(w + 4)

p(w) = 4w + 16

Problem 2 :

Which equation represents the line with a greater slope and lesser y-intercept then than the line shown ?

A)  3x - y = 4     B)  x - 2y = -12     C) 9x + 2y = -10

D)  5x + 3y  = 30

Solution :

So, option A is correct.

Problem 3 :

Which expression is equivalent to 49x² - 36 ?

A)  (7x - 6) (7x + 6)         B)  (7x - 6) (7x - 6)

C)  (49x + 36) (49x - 36)         D)  (x - 6) (x + 7)

Solution :

49x² - 36

= (7x)² - 6²

= (7x + 6)(7x - 6)

Problem 4 :

The area of the base of a pyramid and its height are related by the formula V = 1/3 Bh

• B is the base of the pyramid
• h is the height of the 

Which equation finds h, given V by B

A) h = V/3B      B)  h = 3V/B

C)  h = B/3V      D) h = V - (B/3)

Solution :

V = 1/3 Bh

Bh = 3V

h = 3V/B

So, option B is correct.

Problem 5 :

The soccer team is selling t-shirts and hats at the foot ball game to earn money.

• 12 t-shirts and 5 hats will sell for $201
• 6 t-shirts and 9 hats will sell for $159

How much does each t-shirt sell for ?

Solution :

Cost of each t-shirt = x, cost of each hat = y

12x + 5y = 201 -----(1)

6x + 9y = 159 -----(2)

(1) - 2(2)

12x + 5y - 12x - 18y = 201-2(159)

-13y = -117

y = 9

Applying y = 9 in (2), we get 

6x + 9(9) = 159

6x = 159 - 81

6x = 78

x = 13

Cost of each t-shirt is $13.

Problem 6 :

Five times Jeff's age plus three times Karen's age equals 92. Karen's age is four more than Jeff's age. How old is Karen ?

Solution :

Let x be Jeff's age. Karen's age = x+4

5x + Karen's age = 92

5x + 3(x + 4) = 92

5x + 3x + 12 = 92

8x = 92 - 12

8x = 80

x = 10

Karen's age = 14

Problem 7 :

Compare the y-intercept of the equation 3x-2y = 14 to the y-intercept in the table. What is the sum of two y-intercepts ?

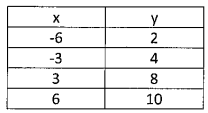
Solution :

3x - 2y = 14

y-intercept from the equation above,

put x = 0

-2y = 14

y = -7

From the table :

Selecting two points (-6, 2) and (-3, 4)

m = (4 - 2) / (-3 + 6)

m = 2/3

y = (2/3)x + b

The line is passing through the point (-6, 2).

2 = (2/3) (-6) + b

2 = -4 + b

b = 6

Difference between y-intercepts = -7 - 6

= -13

Problem 8 :

What is an x-intercept of the graph of the function 

f(x) = x² - 14x + 49 ?

Solution :

f(x) = x² - 14x + 49

x-intercept, put y = 0

x² - 14x + 49 = 0

x² - 7x - 7x + 49 = 0

x(x - 7) -7(x - 7) = 0

(x - 7) (x - 7) = 0

x = 7, x = 7

Problem 9 :

What is the largest three consecutive positive integers if the sum of twice the smallest and the middle integers is equal to twice the largest integer ?

Solution :

Let x, x + 1 and x + 2 are three consecutive positive integers.

2x + x + 1 = 2(x + 2)

3x + 1 = 2x + 4

3x - 2x = 4 - 1

x = 3

Largest number = 3 + 2 ==> 5

Problem 10 :

The function h(t) = -2t² - 7t + 15 models the approximate height of an object at time t. How many seconds will it take the object to hit the ground ?

Solution :

h(t) = -2t² - 7t + 15

When it will hit the ground, h(t) = 0

-2t² - 7t + 15 = 0

-2t² - 10t + 3t + 15 = 0

-2t(t + 5) + 3(t + 5) = 0

(-2t + 3)(t + 5) = 0

t = 3/2, t = -5

It will hit the ground after 1.5 seconds.

Problem 11 :

The function h(t) = -16x² + 64x + 5 represents the height of the object at time x. What is the maximum height of the object reaches ?

Solution :

h(t) = -16x² + 64x + 5

To find the maximum value, we have to express the given quadratic function from standard form to vertex form.

h(t) = -16[x² - 4x] + 5

= -16[x² - 2(x)(2) + 2² - 2²] + 5

= -16[(x - 2)² - 4] + 5

= (x - 2)² + 64 + 5

= (x - 2)² + 69

Vertex is (2, 69). So, the maximum height is 69.

Problem 12 :

The function P(x) = 3500 (0.75)^x represents the cost of computer x years after it has been purchased. What percentage of the cost of the computer decreasing each year?

Solution :

P(x) = 3500 (0.75)^x

1 - r% = 0.75

r% = 1 - 0.75

r% = 0.25

r% = 25%

25% is decreasing percentage.