10TH GRADE ALGEBRA 1 PRACTICE QUESTIONS

Problem 1 :

Line segment KL is shown on this coordinate plane

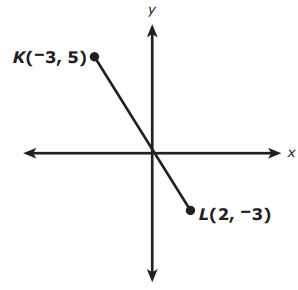
What are the coordinates of the midpoint of line segment KL?

A) (−1, 1/2 )    B) (−1/2 , 1)   C) (1/2 , −1)   D) (1, −1/2 )

Solution :

So, option B is correct.

Problem 2 :

Shayla and Carlos each have a bag that contains 5 green marbles, 5 red marbles, and 10 yellow marbles. The marbles are all the same size and shape.

Part A :

Shayla will select two marbles from her bag at random. She will not return the first marble to the bag before selecting the second marble.

Which expression represents the probability that Shayla will select two red marbles?

A) 5/20, 4/19    B) 5/20, 4/20    C) 5/20, 5/19   D) 5/20, 5/20

Part B :

Carlos will select two marbles from his bag at random. He will not return the first marble to the bag before selecting the second marble. The first marble Carlos selects will not be yellow.

What is the probability that the second marble he selects will be yellow?

A) 9/20    B) 9/19    C) 10/20     D) 10/19

Solution :

Part A :

Total number of marbles =  5 green + 5 red + 10 yellow

= 20 marbles

Probability of selecting 1 red marble = 5/20

She will not return the marble that she has selecting.

Probability of selecting 1 red marble = 4/19

So, option A is correct.

Part B :

After selecting the first marble, probability of selecting the marble which is yellow = 9/20

Problem 3 :

What are the solutions of this equation?

x² + 7x + 12 = 0

A) x = −3; x = −4        B) x = −2; x = −6

C) x = 2; x = 6        D) x = 3; x = 4

Solution :

x² + 7x + 12 = 0

x² + 3x + 4x + 12 = 0

x(x + 3) + 4(x + 3) = 0

(x + 4)(x + 3) = 0

x + 4 = 0 and x + 3 = 0

x = -4 and x = -3

So, option A is correct.

Problem 4 :

This double bar graph shows the amounts of time, in minutes, an athlete spent on aerobic training and strength training each day for 5 days.

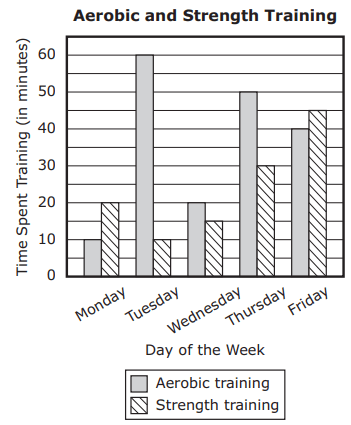
A. On what day did the athlete spend the longest total amount of time training? Show or explain how you got your answer.

B. What is the median total number of minutes the athlete spent training each day? Show or explain how you got your answer.

C. What percent of the total number of minutes the athlete spent training for the 5 days was spent on strength training? Show or explain how you got your answer.

D. Determine whether the sum of the mean number of minutes spent on aerobic training and the mean number of minutes spent on strength training is equal to the mean total number of minutes spent training. Show or explain how you got your answer.

Solution :

Question A :

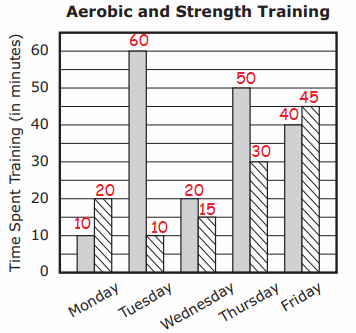
Time taken for practice on weekdays :

Monday = 10 + 20 ==> 30 minutes

Tuesday = 60 + 10 ==> 70 minutes

Wednesday = 20 + 15 ==> 35 minutes

Thursday = 50 + 30 ==> 80 minutes

Friday = 40+45 ==> 85 minutes

On Friday, he did long time practice.

Question B :

Arranging the above minutes in ascending order, we get

30, 35, 70, 80, 85

So, the median is 70.

Question C :

Total number of minutes of training = 30 + 35 + 70 + 80 + 85

= 300

Time taken for strength training = 20 + 10 + 15 + 30 + 45

= 120

Fraction of time taken for strength in total = 120/300

= 2/5

Question D :

Mean number of minutes for Aerobic training

= (10 + 60 + 20 + 50 + 40)/5

= 180/5

= 36

Mean number of minutes for strength training

= (20 + 10 + 15 + 30 + 45)/5

= 120/5

= 24

Sum of mean number of minutes for Aerobic and strength training = 36 + 24

= 60 ----(1)

Mean number of minutes spent of training

= (30+35+70+80+85)/5

= 300/5

= 60 ----(2)

So, they are equal.

Problem 5 :

A rectangular garden that is 16 1/4 feet wide and 11 3/4 feet long will be covered with soil. If a bag of soil covers an area of 20 square feet, which of the following is closest to the number of bags of soil needed to cover the garden?

A) 2    B) 3    C) 8    D) 10

Solution :

Area of the rectangular garden = length x width

= 16  1/4 x 11  3/4

= (65/4) x (47/4)

= 3055/16 square feet

A bag of soil can cover 20 square feet

Number of bags needed = (3055/16) / 20

= 9.54

Approximately 10 bags are needed. So, option D is correct.

Problem 6 :

Four triangles and some of their angle measures are shown.

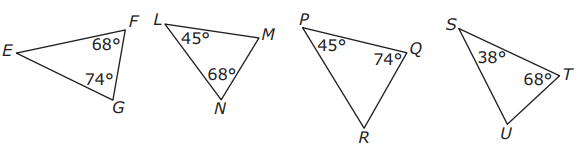
Based on the angle measures, which of the following similarity statements is true?

A) ΔFGE ~ ΔTUS         B) ΔGEF ~ ΔQPR

C) ΔLMN ~ ΔPQR        D) ΔNML ~ ΔTSU

Solution :

In triangle EFG, finding the missing angle.

∠E+∠F+∠G = 180

∠E + 68 + 74 = 180

∠E = 180 - 142

∠E = 38

In triangle EFG, finding the missing angle.

∠S+∠T+∠U = 180

38 + 68 + ∠U = 180

∠U = 180 - 106

∠U = 74

So, triangles ΔFGE and ΔTUS are similar. Option A is correct.

Problem 7 :

These two triangles are similar.

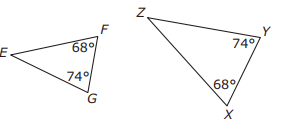
Which of the following similarity statements about the triangles are true? Select the two true statements.

A) ΔEFG ~ ΔZYX       B) ΔEGF ~ ΔXYZ   C) ΔFEG ~ ΔXZY

D) ΔFGE ~ ΔYZX       E) ΔGFE ~ ΔYXZ

Solution :

Finding the missing angle in triangle EFG,

∠E + ∠F + ∠G = 180

∠E + 68 + 74 = 180

∠E = 180 - 142

∠E = 38

The sides which is opposite to equal angle measures will be equal.

FG = YX

EG = ZY

EF = ZX

Option E is correct.

Problem 8 :

Which of the following is equivalent to this expression?

x² + 5x − 84

A) (x + 6)(x − 14)      B) (x − 6)(x + 14)

C) (x + 7)(x − 12)      D) (x − 7)(x + 12)

Solution :

= x² + 5x − 84

= x² + 12x - 7x − 84

= x (x + 12) - 7(x + 12)

= (x - 7) (x + 12)

So, option C is correct.