10TH ALGEBRA 1 MATH PRACTICE QUESTIONS

Problem 1 :

Which of the following is equivalent to this expression?

−5x(−6x² + 1)

A) 30x³ − 4x     B) 30x³ − 5x    C) −11x³ − 4x     D −11x³ − 5x

Solution :

Using distributive property, 

= -5x (−6x²) - 5x(1)

= 30x³ - 5x

Problem 2 :

Consider this function.

f(x) = x(18 − x)

What are the values of f(0), f(5), and f(18)?

A) f(0) = −18 f(5) = 90 f(18) = −36

B) f(0) = 0 f(5) = 90 f(18) = −324

C) f(0) = 0 f(5) = 65 f(18) = 0

D) f(0) = 18 f(5) = −450 f(18) = −36

Solution :

f(x) = x(18 − x)

Evaluating f(18) :

Applying x as 18, we get

f(18) = 18(18 - 18)

f(18) = 18(0)

= 0

So, option C is correct.

Problem 3 :

This diagram shows a circle with an inscribed right triangle and some of its measurements, in units.

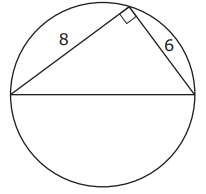
Based on the diagram, what is the circumference, in units, of the circle?

A) 5π     B) 10π    C) 14π    D) 25π

Solution :

The semicircle will make 90 degree angle measure on the circumference of the circle. By finding hypotenuse of the right triangle, we get the length of the diameter of the circle.

Let d be the length of diameter.

8² + 6² = d²

d² = 64 + 36

d² = 100

d = 10

Circumference of the circle = πd

= 10π

Problem 4 :

On a coordinate plane, a single transformation will be performed on square RSTU. Select three transformations of square RSTU that would result in a congruent figure.

A) a translation 3 units up and 8 units to the right

B) a rotation of 270° counterclockwise about the origin

C) a dilation by a scale factor of 1 with respect to the origin

D) a dilation by a scale factor of 1.5 with respect to the origin

E) a dilation by a scale factor of −2 with respect to the origin

Solution :

Dilation of scale factor is 1:

ratio between old figure to new figure is 1 : 1

So, option C is correct.

Problem 5 :

Consider this system of equations.

h + c = 2.25

h − c = 1.75

What value of h makes the system of equations true?

Solution :

h + c = 2.25 ----(1)

h − c = 1.75 ---(2)

c = h - 1.75

Applying the value of c in (1), we get

h + h - 1.75 = 2.25

2h - 1.75 = 2.25

2h = 2.25 + 1.75

2h = 4

h = 2

So, the value of h is 2.

Problem 6 :

Which of the following is equivalent to this expression?

4k⁴ + 16k³ + 10k²

A) 4k²(k² + 4k + 2)            B) 2k²(2k² + 8k + 5) 

C) 2(2k⁴ + 14k³ + 8k²)      D) 2k²(2k² + 16k + 10)

Solution :

= 4k⁴ + 16k³ + 10k²

Factoring 2k²,

= 2k²(2k² + 8k + 5)

So, option B is correct.

Problem 7 :

Consider this inequality. y ≥ x − 4 Which of the following graphs represents the solution set of the inequality?

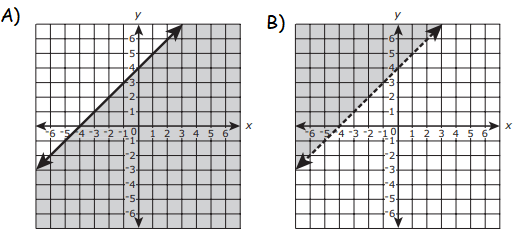
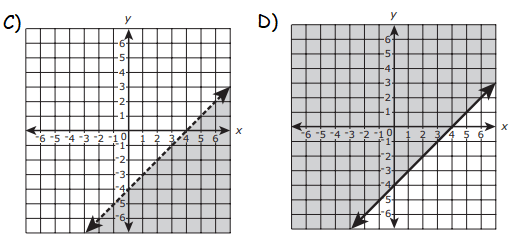
y ≥ x − 4

To graph the line, we can make it as equation.

y = x - 4

Slope m = 1 (raising line) and y-intercept (b) = -4

Since we have grater than or equal sign, we have to use the solid line. Either Option A or D.

y ≥ x − 4

Choosing one of the points from the shaded region from Option A :

Choosing one of the points from the shaded region from Option D :

So, option D is correct.

Problem 8 :

Line w is represented by this equation. y = 5x + 3 Which of the following equations represents a line that is perpendicular to line w?

A) y = − (1/5)x + 1     B) y = −5x + 1

C) y = 1/5x + 1       D) y = 5x + 1

Solution :

y = 5x + 3

If two lines are perpendicular, then the product of their slopes will be equal to -1.

y = 5x + 3

y = mx + b 

m = 5

Slope of the line which is perpendicular to the given line = -1/5

From the given options, option A is having the slope -1/5.

Problem 9 :

A line and a parabola are graphed on a coordinate plane. The equation of the line and the equation of the parabola are shown in this table.

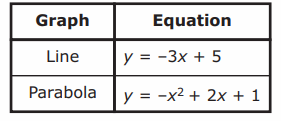
A. What is the value of y for the line when x = −4? Show or explain how you got your answer.

B. What is the value of y for the parabola when x = −4? Show or explain how you got your answer.

C. The line and the parabola intersect at two points. The distance, in units, between the two points is represented by this expression.

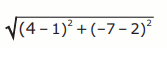
Simplify the expression to determine the distance, in units, between the two points. Show or explain how you got your answer.

D. The area, in square units, of the region on the coordinate plane enclosed by the parabola and the line is represented by this expression.

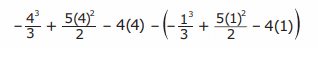
Solution :

Question A :

At x = −4, the value of y on the line is

y = -3(-4) + 5

y = -12 + 5

y = -7

Question B :

When x = -4

y = -x² + 2x + 1

y = -(-4)² + 2(-4) + 1

y = -16 - 8 + 1

y = -24 + 1

y = -23

Question C :

Question D :

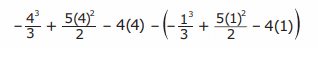
Problem 10 :

A waiter recorded the amount of money he earned in tips each weekday for a two-week period. His data are shown in this table.

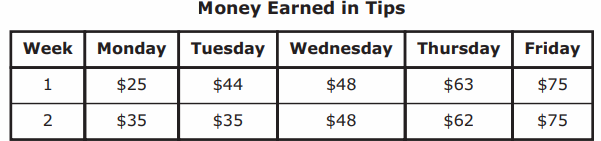
Which statement about the data in the table is true?

A. The median and the range for week 1 are equal to the median and the range for week 2.

B. The median and the mode for week 1 are equal to the median and the mode for week 2.

C The mean and the median for week 1 are equal to the mean and the median for week 2.

D The mean and the range for week 1 are equal to the mean and the range for week 2.

Solution :

To analyze which statement is true, we have to find mean, median, mode and range of the given data. 

Median of Week 1 = 48

Median of Week 2 = 48

Mode of week 1 :

No quantity is repeated. So, there is no mode

Mode of week 2 :

Mode of week 2 is 35.

Range of week 1 = 75 - 22

= 53

Range of week 2 = 75 - 35

= 40

Then option C is correct.